ما هي التحولات الأولية التي يمكن إجراؤها باستخدام المصفوفة. جبر المصفوفات - التحولات الأولية للمصفوفات. المصفوفات، أنواع المصفوفات، العمليات على المصفوفات

ابتدائيتحويلات السلسلةتسمى المصفوفات تحويلات من الأنواع التالية:

1) ضرب كل عنصر من عناصر السلسلة بنفس الرقم غير الصفر. تبقى الأسطر المتبقية دون تغيير (باختصار: ضرب سطر برقم).

2) إضافة إلى كل عنصر من عناصر سطر معين العناصر المقابلة له من سطر آخر مضروبة في نفس العدد. تبقى الأسطر المتبقية (بما في ذلك السطر الذي تتم إضافته) دون تغيير (باختصار: إضافة سطر آخر إلى سطر، مضروبًا في رقم).

3) قم بتبديل صفين من المصفوفة. تبقى الخطوط المتبقية دون تغيير.

وتسمى هذه التحولات على التوالي التحولات الأولى , ثانية و النوع الثالث (نوعا ما ). بتطبيقها بالتتابع، نحصل على تحويلات أكثر تعقيدا.

محددة بالمثل تحويلات الأعمدة الأولية المصفوفات.

نظرية

التحويل من النوع الثالث هو مزيج من التحويلات من النوعين الأول والثاني.

وهكذا يمكن تصنيف التحولات من النوع الثالث على أنها أكثر تعقيدا من التحويلات الأولية. لكنها لا تزال تعتبر أساسية من أجل الراحة.

نظرية

يمكن اختزال أي مصفوفة إلى مصفوفة خطوة عن طريق تحويلات الصف الأولية. إذا طبقنا التحويلات الأولية للصفوف والأعمدة على المصفوفة, ومن ثم يمكن اختزاله إلى شكل شبه منحرف.

على سبيل المثال,

á(1) تبديل السطر الأول والثاني (التحويل من النوع الثالث).

(2) السطر الأول مضروبا في 2 يضاف إلى الثاني ويطرح من الثالث مضروبا في 3 يضاف إلى الرابع (تحويلات النوع الثاني).

(3) طرح السطر الثاني من الثالث وطرح السطر الثاني مضروبا في 14/11 من الرابع.

(4) بدل السطر الثالث والرابع.ñ

وهكذا قمنا بتحويل المصفوفة الأصلية

بطريقة تدريجية

الآن بعد تبديل العمودين الثاني والثالث، ثم تبديله مع العمود الرابع، ننقل العمود الثاني إلى مكان الرابع، وسيكون العمودان الثالث والرابع في مكان العمودين الثاني والثالث على التوالي:

وبالتالي تحويل المصفوفة الأصلية إلى شبه منحرف.

تمارين

إحضار المصفوفة إلى أشكال متدرجة وشبه منحرفة:

يتم استدعاء العمليات الثلاث التالية التحولات الأولية لصفوف المصفوفة:

1) الضرب الخط الأولمصفوفات العدد lect ≠ 0 :

والتي سنكتبها بالصيغة (i) → lect(i).

2) تبديل صفين في المصفوفة، على سبيل المثال الصفين i-th وk-th:

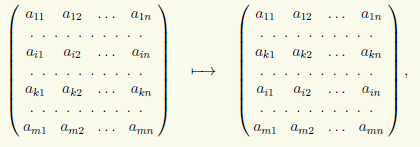
والتي سنكتبها على الشكل (ط) ↔ (ك).

3) إضافة إلى الصف i من المصفوفة الصف k مع المعامل lect:

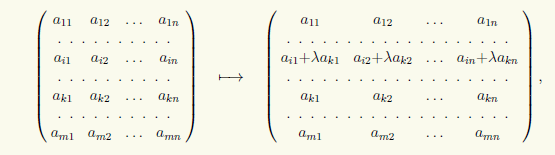
والتي سنكتبها بالصيغة (i) → (i) + lect(k).

تسمى العمليات المماثلة على أعمدة المصفوفة تحويلات الأعمدة الأولية.

كل تحويل أولي لصفوف أو أعمدة المصفوفة له التحول الأولي العكسي، الذي يحول المصفوفة المحولة إلى المصفوفة الأصلية. على سبيل المثال، التحويل العكسي لتبديل سلسلتين هو تبديل نفس السلاسل.

يمكن تفسير كل تحويل أولي لصفوف (أعمدة) المصفوفة A على أنه ضرب A على اليسار (اليمين) بمصفوفة من نوع خاص. يتم الحصول على هذه المصفوفة إذا تم إجراء نفس التحويل مصفوفة الهوية. دعونا نلقي نظرة فاحصة على تحويلات السلسلة الأولية.

دع المصفوفة B تكون النتيجة الضرب طصفوف مصفوفة A من النوع m×n بالرقم ω ≠ 0. ثم B = E i (α)A، حيث يتم الحصول على المصفوفة E i (α) من مصفوفة الهوية E من الرتبة m عن طريق ضرب i- الصف الرابع بالرقم LA.

دع المصفوفة B يتم الحصول عليها كنتيجة لتبديل الصفين i-th و k من المصفوفة A من النوع m×n. ثم B = F ik A، حيث يتم الحصول على المصفوفة F ik من مصفوفة الهوية E من الرتبة m عن طريق تبديل صفيها i-th وk-th.

دع المصفوفة B يتم الحصول عليها عن طريق إضافة الصف k الخاص بها مع المعامل lect إلى الصف i من المصفوفة m×n A. ثم B = G ik (α)А، حيث يتم الحصول على المصفوفة G ik من مصفوفة الهوية E من الرتبة m عن طريق إضافة الصف k مع المعامل α إلى الصف i، أي. عند تقاطع الصف i والعمود k من المصفوفة E، يتم استبدال عنصر الصفر بالرقم lect.

يتم تنفيذ التحويلات الأولية لأعمدة المصفوفة A بنفس الطريقة تمامًا، ولكن في نفس الوقت يتم ضربها بمصفوفات من نوع خاص ليس على اليسار، ولكن على اليمين.

باستخدام الخوارزميات التي تعتمد على التحويلات الأولية للصفوف والأعمدة، يمكن تحويل المصفوفات إلى أنواع مختلفة. تشكل إحدى أهم هذه الخوارزميات أساس إثبات النظرية التالية.

نظرية 10.1.باستخدام تحويلات الصف الأولية، يمكن اختزال أي مصفوفة إلى عرض متدرج.

◄ برهان النظرية يتمثل في البناء خوارزمية محددةجلب المصفوفة إلى شكل تدريجي. تتكون هذه الخوارزمية من تكرار ثلاث عمليات بشكل متكرر وبترتيب معين مرتبطة ببعض عناصر المصفوفة الحالية، والتي يتم تحديدها بناءً على موقعها في المصفوفة. في الخطوة الأولى من الخوارزمية، نختار العنصر العلوي الأيسر باعتباره العنصر الحالي في المصفوفة، أي. [أ] 11 .

1*. إذا كان العنصر الحالي صفراً، انتقل إلى العملية 2*. وإذا لم يكن يساوي الصفر، فيتم إضافة الصف الذي يقع فيه العنصر الحالي (الصف الحالي) بالمعاملات المناسبة إلى الصفوف الموجودة أدناه، بحيث تصبح جميع عناصر المصفوفة في العمود الموجود تحت العنصر الحالي صفراً. على سبيل المثال، إذا كان العنصر الحالي هو [A] ij، إذن كمعامل للصف k، k = i + 1, ... ، يجب أن نأخذ الرقم - [A] kj /[A] ij . نختار عنصرًا حاليًا جديدًا، ونتحرك في المصفوفة عمودًا واحدًا إلى اليمين وصفًا واحدًا لأسفل، وننتقل إلى الخطوة التالية، ونكرر العملية 1*. إذا كان هذا التحول غير ممكن، أي. تم الوصول إلى العمود أو الصف الأخير، نتوقف عن التحويل.

2*. إذا كان العنصر الحالي في بعض صفوف المصفوفة يساوي الصفر، فإننا ننظر إلى عناصر المصفوفة الموجودة في العمود أسفل العنصر الحالي. إذا لم يكن هناك أي أرقام غير صفرية بينهم، فإننا ننتقل إلى العملية 3*. اتركه خط كيوجد عنصر غير الصفر أسفل العنصر الحالي. مبادلة الحالية و خط كوالعودة إلى العملية 1*.

3*. إذا كان العنصر الحالي وجميع العناصر التي تحته (في نفس العمود) تساوي صفر، نقوم بتغيير العنصر الحالي، مع تحريك عمود واحد إلى اليمين في المصفوفة. إذا كان مثل هذا التحول ممكنا، أي أن العنصر الحالي ليس في العمود الموجود في أقصى يمين المصفوفة، فإننا نكرر العملية 1*. إذا وصلنا بالفعل إلى الحافة اليمنى للمصفوفة وكان تغيير العنصر الحالي مستحيلا، فإن المصفوفة لها شكل متدرج، ويمكننا التوقف عن التحويل.

بما أن المصفوفة محدودة أبعاد، وفي خطوة واحدة من الخوارزمية يتم إزاحة موضع العنصر الحالي إلى اليمين بواسطة عمود واحد على الأقل، وستنتهي عملية التحويل، وفي ما لا يزيد عن n خطوة (n هو عدد الأعمدة في المصفوفة). هذا يعني أنه ستأتي لحظة سيكون فيها للمصفوفة شكل متدرج.

مثال 10.10.دعونا نحول المصفوفة إلى نموذج القيادة باستخدام تحويلات السلسلة الأولية.

باستخدام الخوارزمية من برهان النظرية 10.1 وكتابة المصفوفات بعد إتمام عملياتها نحصل على

تحويلات المصفوفة الأولية- هذه هي تحويلات المصفوفة، ونتيجة لذلك يتم الحفاظ على تكافؤ المصفوفات. وبالتالي، فإن التحويلات الأولية لا تغير مجموعة حلول نظام المعادلات الجبرية الخطية الذي تمثله هذه المصفوفة.

تُستخدم التحويلات الأولية في الطريقة الغوسية لتقليل المصفوفة إلى شكل مثلث أو شكل متدرج.

تعريف

تحويلات السلسلة الأوليةوتسمى:

في بعض مقررات الجبر الخطي، لا يتم تمييز تبديل صفوف المصفوفات على أنه تحويل أولي منفصل نظرًا لأنه يمكن الحصول على تبديل أي صفين من المصفوفات عن طريق ضرب أي صف مصفوفة في ثابت، وإضافة صف آخر إلى أي صف مصفوفة مضروبًا بواسطة ثابت، .

محددة بالمثل تحويلات الأعمدة الأولية.

التحولات الأولية تفريغ.

يشير الترميز إلى أنه يمكن الحصول على المصفوفة عن طريق التحويلات الأولية (أو العكس).

ملكيات

ثبات الرتبة في ظل التحولات الأولية

معادلة SLAEs في ظل التحولات الأولية

لنتصل التحولات الأولية على نظام المعادلات الجبرية الخطية :

• إعادة ترتيب المعادلات؛
• ضرب المعادلة بثابت غير الصفر؛
• إضافة معادلة إلى أخرى، مضروبة في بعض الثوابت.

أولئك. التحولات الأولية على مصفوفتها الموسعة. إذن العبارة التالية صحيحة: تذكر أن النظامين يطلق عليهما اسم مكافئ إذا كانت مجموعات الحلول الخاصة بهما متطابقة.

إيجاد المصفوفات العكسية

نظرية (حول إيجاد المصفوفة العكسية). دع محدد المصفوفة يكون غير صفر، دع المصفوفة يتم تعريفها بالتعبير. بعد ذلك، أثناء التحول الأولي لصفوف المصفوفة إلى مصفوفة الهوية في التكوين، يحدث التحول في نفس الوقت.

تخفيض المصفوفات إلى شكل الصف

دعونا نقدم مفهوم المصفوفات الخطوة: المصفوفة لديها عرض متدرج ، إذا: فإن العبارة التالية صحيحة:

التعريفات ذات الصلة

مصفوفة ابتدائية.تعتبر المصفوفة A أولية إذا كان ضرب المصفوفة العشوائية B بها يؤدي إلى تحويلات أولية للصفوف في المصفوفة B.

الأدب

إيلين في.أ.، بوزنياك إي.جي. الجبر الخطي: كتاب مدرسي للجامعات. - الطبعة السادسة، محذوفة. - م: فيزماتليت، 2004. - 280 ص.

مؤسسة ويكيميديا. 2010.

انظر ما هي "تحويلات المصفوفة الأولية" في القواميس الأخرى:

مقدمة. E. الجسيمات بالمعنى الدقيق لهذا المصطلح هي جسيمات أولية غير قابلة للتحلل، والتي تتكون منها كل المادة، حسب الافتراض. في الحديث مصطلح الفيزياء "E. ح." عادة لا يستخدم بمعناه الدقيق، ولكن بشكل أقل صرامة بالنسبة للاسم... ... الموسوعة الفيزيائية

مقدمة. E. الجسيمات بالمعنى الدقيق لهذا المصطلح هي جسيمات أولية غير قابلة للتحلل، والتي تتكون منها كل المادة، حسب الافتراض. في مفهوم "E. ح." في الفيزياء الحديثة تجد فكرة الكيانات البدائية تعبيرا... ... الموسوعة السوفيتية الكبرى

هذا المصطلح له معاني أخرى، انظر ماتريكس. المصفوفة هي كائن رياضي مكتوب على شكل جدول مستطيل لعناصر حلقة أو حقل (على سبيل المثال، أعداد صحيحة أو حقيقية أو أرقام مركبة) يمثل ... ... ويكيبيديا

المصفوفة هي كائن رياضي مكتوب على شكل جدول مستطيل من الأرقام (أو عناصر حلقة) ويسمح بإجراء العمليات الجبرية (الجمع والطرح والضرب وغيرها) بينها وبين كائنات أخرى مماثلة. قواعد التنفيذ... ... ويكيبيديا

المصفوفة هي كائن رياضي مكتوب على شكل جدول مستطيل من الأرقام (أو عناصر حلقة) ويسمح بإجراء العمليات الجبرية (الجمع والطرح والضرب وغيرها) بينها وبين كائنات أخرى مماثلة. قواعد التنفيذ... ... ويكيبيديا

المصفوفة هي كائن رياضي مكتوب على شكل جدول مستطيل من الأرقام (أو عناصر حلقة) ويسمح بإجراء العمليات الجبرية (الجمع والطرح والضرب وغيرها) بينها وبين كائنات أخرى مماثلة. قواعد التنفيذ... ... ويكيبيديا

المصفوفة هي كائن رياضي مكتوب على شكل جدول مستطيل من الأرقام (أو عناصر حلقة) ويسمح بإجراء العمليات الجبرية (الجمع والطرح والضرب وغيرها) بينها وبين كائنات أخرى مماثلة. قواعد التنفيذ... ... ويكيبيديا

المصفوفة هي كائن رياضي مكتوب على شكل جدول مستطيل من الأرقام (أو عناصر حلقة) ويسمح بإجراء العمليات الجبرية (الجمع والطرح والضرب وغيرها) بينها وبين كائنات أخرى مماثلة. قواعد التنفيذ... ... ويكيبيديا

التحويلات الأولية هي الإجراءات التالية على صفوف وأعمدة المصفوفة A:

1) مبادلة صفين أو عمودين من المصفوفة؛

2) ضرب صف أو عمود من المصفوفة برقم غير الصفر؛

3) إضافة صف (عمود) آخر إلى صف واحد (عمود).

نظرية.لا تغير التحويلات الأولية رتبة المصفوفة، أي إذا تم الحصول على المصفوفة B من المصفوفة A عن طريق التحويلات الأولية، إذن.

دليل. 1). عند تبديل عمودين من المصفوفة، لا يتغير الحد الأقصى لعدد الأعمدة المستقلة خطيًا، وبالتالي لا يتغير ترتيبها.

2). دع المصفوفة B يتم الحصول عليها من المصفوفة A عن طريق ضرب الصف i بالرقم t0 و r(A) =k. من الواضح أن أي قاصر من المصفوفة B لا يحتوي على الصف i يساوي القاصر المقابل للمصفوفة A، وأي قاصر من المصفوفة B يحتوي على الصف i يساوي القاصر المقابل للمصفوفة A مضروبًا في الرقم t. وبالتالي، فإن القاصر من الرتبة k للمصفوفة B، الموافق للأساس القاصر للمصفوفة A، سيكون غير صفر، وجميع القاصرين من الرتبة k+1 للمصفوفة B، وكذلك جميع القاصرين من الرتبة k+1 للمصفوفة أ، سوف يساوي الصفر. هذا يعني أن r(B)=k=r(A).

3). دع المصفوفة B يتم الحصول عليها من المصفوفة A عن طريق إضافة الصف i إلى الصف j و r (A) = k. سوف تكون العناصر الثانوية من الرتبة k+1 للمصفوفة B التي لا تحتوي على الصف j مساوية للعناصر الثانوية المقابلة للمصفوفة A، وبالتالي تساوي الصفر. العناصر الثانوية من الرتبة k+1 للمصفوفة B التي تحتوي على الصفين i وj ستكون مساوية لمجموع محددين صفريين. يحتوي أحد هذه المحددات على صفين متطابقين (يحتوي الصف j على عناصر الصف i)، والمحدد الثاني هو صغير من الرتبة k+1 للمصفوفة A وبالتالي يساوي الصفر. الثانوية من الرتبة k+1 من المصفوفة B، التي تحتوي على الصف j، ولكن لا تحتوي على الصف i، ستكون مساوية لمجموع اثنين من الرتب الثانوية k+1 من المصفوفة A وبالتالي ستكون مساوية أيضًا لـ صفر. وبالتالي، فإن جميع العناصر الثانوية من الرتبة k+1 للمصفوفة B تساوي 0 و r(B)k=r(A).

لنحصل على المصفوفة C من المصفوفة B بضرب الصف i في (-1). ثم يتم الحصول على المصفوفة A من المصفوفة C عن طريق إضافة الصف i إلى الصف j وضرب الصف i في (-1). لذلك، كما ثبت أعلاه، سيكون هناك r(A)r(C) =r(B). وبالتالي، فإن المتباينات r(B)r(A) وr(A)r(B) صالحة في نفس الوقت، مما يعني أن r(A) =r(B).

تُستخدم خاصية التحويلات الأولية هذه عمليًا لحساب رتبة المصفوفة. للقيام بذلك، باستخدام التحويلات الأولية، نقوم بتقليل هذه المصفوفة (غير الصفر) A إلى شكل شبه منحرف، أي إلى الشكل

ب= ,

حيث العناصر للجميع i = 1,2,...,k; عناصر للجميع i > j و

أنا > ك. من الواضح أن r(B) = k، أي أن رتبة المصفوفة B تساوي عدد الصفوف غير الصفرية. يأتي هذا من حقيقة أن الترتيب الصغير k للمصفوفة B، الموجود عند تقاطع الصفوف والأعمدة الأولى k، هو محدد قطري ويساوي؛ وأي قاصر من الترتيب k+1 من المصفوفة B يحتوي على صف صفر، مما يعني أنه يساوي 0 (أو، إذا كان k = n، لا يوجد مثل هذه القاصرين على الإطلاق).

نظرية.يمكن اختزال أي مصفوفة غير صفرية A ذات البعد mn إلى شكل شبه منحرف باستخدام التحويلات الأولية.

دليل.بما أن A0، يوجد عنصر مصفوفة
. من خلال تبديل الصف الأول والعمود الأول والعمود j، نقوم بتحريك العنصر إلى الزاوية اليسرى العليا من المصفوفة والدلالة
. ثم إلى الصف الأول من المصفوفة الناتجة (i= 2,3, ...,m) نضيف الصف الأول مضروبًا في الرقم . ونتيجة لهذه التحولات الأولية، نحصل على المصفوفة

أ
.

إذا كانت جميع العناصر
المصفوفات A تساوي صفراً، ثم يتم إثبات النظرية. إذا كان هناك عنصر
، بعد ذلك، من خلال إعادة ترتيب الصفين الثاني والأول، والعمودين الثاني والي للمصفوفة A، نقوم بتحريك العنصر بدلا من العنصر وتدل
(لو
، ثم نشير إليه على الفور
). ثم إلى الصف الأول من المصفوفة الناتجة (i= 3, ...,m) نضيف الصف الثاني مضروبًا في الرقم . ونتيجة لذلك، نحصل على المصفوفة

.

بمواصلة هذه العملية، في عدد محدود من الخطوات نحصل على المصفوفة B، أي أننا نقوم بتقليل المصفوفة A إلى شكل شبه منحرف.

مثال.دعونا نحسب رتبة المصفوفة



. تشير الأسهم إلى التحولات الأولية التالية: 1) تم تبديل السطرين الأول والثاني؛ 2) إضافة ثلث إلى السطر الرابع؛ 3) أضف السطر الأول مضروبًا في -2 إلى السطر الثالث، وقسم السطر الرابع على 3؛ 4) قسمت السطر الثالث على 5 وبدلت السطرين الثالث والرابع؛ 5) أضيف سطر ثان إلى السطر الثالث مضروبا في -3 وأضيف ثالث إلى السطر الرابع. يمكن ملاحظة أن المصفوفة التي تم الحصول عليها من المصفوفة A بواسطة التحولات الأولية المشار إليها لها شكل شبه منحرف مع ثلاثة صفوف غير صفرية. ولذلك، ص(أ) = 3.

تحويلات المصفوفة الأولية- هذه هي تحويلات المصفوفة، ونتيجة لذلك يتم الحفاظ على تكافؤ المصفوفات. وبالتالي، فإن التحويلات الأولية لا تغير مجموعة حلول نظام المعادلات الجبرية الخطية الذي تمثله هذه المصفوفة.

تُستخدم التحويلات الأولية في الطريقة الغوسية لتقليل المصفوفة إلى شكل مثلث أو شكل متدرج.

تعريف

تحويلات السلسلة الأوليةوتسمى:

في بعض مقررات الجبر الخطي، لا يتم فصل تبديل صفوف المصفوفة إلى تحويل أولي منفصل نظرًا لحقيقة أنه يمكن الحصول على تبديل أي صفين من المصفوفات عن طريق ضرب أي صف مصفوفة في ثابت ك (\displaystyle ك)، وإضافة صف آخر إلى أي صف من المصفوفة، مضروبًا في ثابت ك (\displaystyle ك), ك ≠ 0 (\displaystyle k\neq 0).

محددة بالمثل تحويلات الأعمدة الأولية.

التحولات الأولية تفريغ.

يشير التدوين إلى أن المصفوفة أ (\displaystyle A)يمكن الحصول عليها من ب (\displaystyle B)من خلال التحولات الأولية (أو العكس).

ملكيات

ثبات الرتبة في ظل التحولات الأولية

نظرية (على ثبات الرتبة في ظل التحولات الأولية). لو أ ∼ ب (\displaystyle A\sim B)، الذي - التي r a n g A = r a n g B (\displaystyle \mathrm (rang) A=\mathrm (rang) B).

معادلة SLAEs في ظل التحولات الأولية

لنتصل التحولات الأولية على نظام المعادلات الجبرية الخطية :

• إعادة ترتيب المعادلات؛
• ضرب المعادلة بثابت غير الصفر؛
• إضافة معادلة إلى أخرى، مضروبة في بعض الثوابت.

أي التحولات الأولية على مصفوفتها الموسعة. إذن العبارة التالية صحيحة: تذكر أن النظامين يسمىان متكافئين إذا كانت مجموعات الحلول الخاصة بهما متطابقة.

إيجاد المصفوفات العكسية

نظرية (حول إيجاد المصفوفة العكسية). دع محدد المصفوفة ا ن × ن (\displaystyle A_(n\times n))لا يساوي الصفر، والسماح للمصفوفة ب (\displaystyle B)يتم تحديده من خلال التعبير ب = [أ | E ] n × 2 n (\displaystyle B=_(n\times 2n)). ثم، مع التحول الأولي لصفوف المصفوفة أ (\displaystyle A)إلى مصفوفة الهوية ه (\displaystyle E)كجزء من ب (\displaystyle B)يحدث التحول في نفس الوقت ه (\displaystyle E)ل ا − 1 (\displaystyle A^(-1)).