ev › Quraşdırma və konfiqurasiya › Matrislə hansı elementar çevrilmələr aparıla bilər. Matris cəbri - matrislərin elementar çevrilmələri. Matris, matrislərin növləri, matrislər üzərində əməliyyatlar

Matrislə hansı elementar çevrilmələr aparıla bilər. Matris cəbri - matrislərin elementar çevrilmələri. Matris, matrislərin növləri, matrislər üzərində əməliyyatlar

İbtidaisimli çevrilmələr matrislərə aşağıdakı növ çevrilmələr deyilir:

1) Sətirin hər bir elementinin eyni sıfırdan fərqli rəqəmə vurulması. Qalan sətirlər dəyişməz olaraq qalır (qısacası: sətri rəqəmə vurmaq).

2) Müəyyən bir xəttin hər bir elementinə başqa bir xəttin uyğun elementlərinin eyni ədədə vurulması. Qalan sətirlər (əlavə olunan da daxil olmaqla) dəyişməz qalır (qısacası: sətirə başqa bir sətir əlavə etmək, nömrə ilə çarpmaq).

3) Matrisin bir neçə iki cərgəsini dəyişdirin. Qalan sətirlər dəyişməz olaraq qalır.

Bu çevrilmələr müvafiq olaraq adlanır birincinin çevrilmələri , ikinci Və üçüncü növ (bir növ ). Onları ardıcıl tətbiq etməklə daha mürəkkəb çevrilmələr əldə edirik.

Eynilə müəyyən edilmişdir elementar sütun çevrilmələri matrislər.

Teorem

Üçüncü növ transformasiya birinci və ikinci növ çevrilmələrin bəzi birləşməsidir.

Beləliklə, üçüncü növ transformasiyalar elementar olanlardan daha mürəkkəb kimi təsnif edilə bilər. Ancaq rahatlıq üçün hələ də elementar hesab olunur.

Teorem

İstənilən matris elementar cərgə çevrilmələri ilə pilləli matrisə endirilə bilər. Əgər matrisə sətir və sütunların elementar çevrilmələrini tətbiq etsək, sonra trapezoidal formaya endirilə bilər.

Misal üçün,

á(1) Birinci və ikinci sətirləri dəyişdirin (üçüncü növün transformasiyası).

(2) 2-yə vurulan birinci sətir ikinciyə əlavə edildi və üçüncüdən çıxarıldı, 3-ə vuruldu, dördüncüyə əlavə edildi (ikinci növ çevrilmələr).

(3) Üçüncüdən ikinci sətir, dördüncüdən isə 14/11-ə vurulan ikinci sətir çıxarıldı.

(4) Üçüncü və dördüncü sətirləri dəyişdirin.ñ

Beləliklə, orijinal matrisi dəyişdirdik

mərhələli şəkildə

İndi ikinci və üçüncü sütunları dəyişdirdikdən sonra dördüncü sütunla əvəz etdikdən sonra ikinci sütunu dördüncü yerinə köçürük, üçüncü və dördüncü sütunlar müvafiq olaraq ikinci və üçüncü sütunların yerində olacaq:

bununla da orijinal matrisi trapesiyaya çevirir.

Məşqlər

Matrisi pilləli və trapezoidal formalara gətirin:

Növbəti üç əməliyyat çağırılır matris sətirlərinin elementar çevrilmələri:

1) Vurma i-ci xəttλ ≠ 0 ədədi üçün matrislər:

(i) → λ(i) şəklində yazacağıq.

2) Matrisdə iki cərgənin dəyişdirilməsi, məsələn, i-ci və k-ci sıralar:

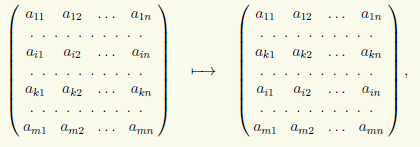
(i) ↔ (k) şəklində yazacağıq.

3) Matrisin i-ci sırasına onun λ əmsallı k-ci cərgəsini əlavə etməklə:

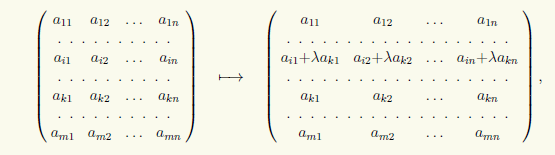
(i) → (i) + λ(k) şəklində yazacağıq.

Matris sütunları üzərində oxşar əməliyyatlar adlanır elementar sütun çevrilmələri.

Bir matrisin satır və ya sütunlarının hər elementar çevrilməsi var tərs elementar çevrilmə, çevrilmiş matrisi orijinala çevirir. Məsələn, iki sətirin dəyişdirilməsi üçün tərs çevrilmə eyni sətirləri dəyişdirməkdir.

A matrisinin sətirlərinin (sütunlarının) hər bir elementar çevrilməsi solda (sağda) A-nın xüsusi formalı matrisa vurulması kimi şərh edilə bilər. Bu matris eyni çevrilmə aparılarsa əldə edilir şəxsiyyət matrisi. Elementar sətir çevrilmələrinə daha yaxından nəzər salaq.

Nəticə B matrisi olsun i-ci vurma m×n tipli A matrisinin sətirləri λ ≠ 0 ədədi ilə. Onda B = E i (λ)A, burada E i (λ) matrisi m düzənli E eynilik matrisindən onun i-ni vurmaqla əldə edilir. λ nömrəsi ilə ci sıra.

m×n tipli A matrisinin i-ci və k-ci sıralarının dəyişməsi nəticəsində B matrisi alınsın. Onda B = F ik A, burada F ik matrisi m sıralı E eynilik matrisindən onun i-ci və k-ci cərgələrini yenidən təşkil etməklə əldə edilir.

m×n A matrisinin i-ci cərgəsinə onun λ əmsallı k-ci cərgəsini əlavə etməklə B matrisi alınsın. Onda B = G ik (λ)А, burada G ik matrisi m düzənli E eynilik matrisindən λ əmsallı k-ci cərgəni i-ci sıraya əlavə etməklə əldə edilir, yəni. E matrisinin i-ci sıra ilə k-ci sütununun kəsişməsində sıfır elementi λ rəqəmi ilə əvəz olunur.

A matrisinin sütunlarının elementar çevrilmələri tamamilə eyni şəkildə həyata keçirilir, lakin eyni zamanda solda deyil, sağda xüsusi tipli matrislərlə vurulur.

Satır və sütunların elementar çevrilməsinə əsaslanan alqoritmlərdən istifadə edərək, matrislər aşağıdakılara çevrilə bilər. müxtəlif növlər. Ən mühüm belə alqoritmlərdən biri aşağıdakı teoremin sübutunun əsasını təşkil edir.

Teorem 10.1. Elementar cərgə çevrilmələrindən istifadə edərək istənilən matrisi kiçildmək olar pilləli görünüş.

◄ Teoremin sübutu qurmaqdan ibarətdir xüsusi alqoritm matrisin pilləli formaya gətirilməsi. Bu alqoritm matrisdə yerləşməsinə görə seçilən bəzi cari matris elementi ilə bağlı üç əməliyyatın müəyyən ardıcıllıqla dəfələrlə təkrarlanmasından ibarətdir. Alqoritmin ilk addımında biz matrisin cari elementi kimi yuxarı sol tərəfi seçirik, yəni. [A] 11 .

1*. Cari element sıfırdırsa, 2* əməliyyatına keçin. Sıfıra bərabər deyilsə, onda cari elementin yerləşdiyi cərgəyə (cari cərgə) aşağıda yerləşən sətirlərə müvafiq əmsallar əlavə edilir ki, cari elementin altındakı sütunun bütün matris elementləri sıfıra çevrilsin. Məsələn, əgər cari element [A] ij , onda k-ci sıra üçün əmsal kimi k = i + 1, ... , biz ədədi götürməliyik - [A] kj /[A] ij . Matrisdə bir sütun sağa və bir sıra aşağı hərəkət edərək yeni bir cari element seçirik və 1* əməliyyatını təkrarlayaraq növbəti addıma keçirik. Belə bir yerdəyişmə mümkün deyilsə, yəni. son sütuna və ya sətirə çatdıqda, transformasiyanı dayandırırıq.

2*. Əgər matrisin hansısa cərgəsindəki cari element sıfıra bərabərdirsə, o zaman cari elementin altındakı sütunda yerləşən matrisin elementlərinə baxırıq. Onların arasında sıfır olmayanlar yoxdursa, 3* əməliyyatına davam edirik. İcazə verin k-ci xətt cari elementin altında sıfırdan fərqli element var. Cari dəyişdirin və k-ci xətt və əməliyyata qayıdın 1*.

3*. Cari element və onun altındakı bütün elementlər (eyni sütunda) sıfıra bərabərdirsə, matrisdə bir sütunu sağa köçürərək cari elementi dəyişirik. Əgər belə bir yerdəyişmə mümkündürsə, yəni cari element matrisin ən sağ sütununda deyilsə, 1* əməliyyatını təkrarlayırıq. Əgər biz artıq matrisin sağ kənarına çatmışıqsa və cari elementi dəyişmək mümkün deyilsə, onda matrisin pilləli forması var və biz çevrilməyi dayandıra bilərik.

Çünki matrisin sonluluğu var ölçüləri, və alqoritmin bir addımında cari elementin mövqeyi ən azı bir sütunla sağa sürüşdürülür, transformasiya prosesi başa çatacaq və n-dən çox olmayan addımda (n - matrisdəki sütunların sayıdır). Bu o deməkdir ki, matrisin pilləli formasına sahib olacağı bir an gələcək.

Misal 10.10. Gəlin matrisi çevirək elementar simli çevrilmələrdən istifadə edərək eşelon formaya.

Teorem 10.1-in isbatından alqoritmdən istifadə edərək və onun əməliyyatlarını tamamladıqdan sonra matrisləri yazaraq əldə edirik.

Elementar matris çevrilmələri- bunlar matrisin çevrilmələridir, nəticədə matrislərin ekvivalentliyi qorunur. Beləliklə, elementar çevrilmələr bu matrisin təmsil etdiyi xətti cəbri tənliklər sisteminin həll çoxluğunu dəyişmir.

Matrisi üçbucaqlı və ya pilləli formaya endirmək üçün Qauss metodunda elementar çevrilmələrdən istifadə edilir.

Tərif

Elementar sətir çevrilmələri adlandırılır:

Bəzi xətti cəbr kurslarında matris sətirlərinin dəyişdirilməsi ayrıca elementar çevrilmə kimi fərqləndirilmir, çünki hər hansı iki matrisin cərgəsinin dəyişdirilməsi istənilən matris cərgəsini sabitə vurmaqla və vurulan istənilən matris sırasına başqa sətir əlavə etməklə əldə edilə bilər. sabitlə,.

Eynilə müəyyən edilmişdir elementar sütun çevrilmələri.

Elementar çevrilmələr geri çevrilə bilən.

Qeyd, matrisin elementar çevrilmələrlə (və ya əksinə) əldə edilə biləcəyini göstərir.

Xüsusiyyətlər

Elementar çevrilmələr altında invariantlığı sıralayın

Elementar çevrilmələrdə SLAE-lərin ekvivalentliyi

zəng edək xətti cəbri tənliklər sistemi üzərində elementar çevrilmələr :

tənliklərin yenidən təşkili;
tənliyi sıfırdan fərqli sabitə vurmaq;
bir tənliyin digərinə əlavə edilməsi, bəzi sabitlərə vurulması.

Bunlar. onun genişləndirilmiş matrisi üzərində elementar çevrilmələr. Onda aşağıdakı müddəa doğrudur: Yada salaq ki, iki sistem onların həll dəstləri üst-üstə düşürsə, ekvivalent adlanır.

Tərs matrislərin tapılması

Teorem (əks matrisin tapılması haqqında).
Matrisin təyinedicisi sıfırdan fərqli olsun, matris ifadəsi ilə müəyyən edilsin. Sonra, matrisin cərgələrinin kompozisiyadakı eynilik matrisinə elementar çevrilməsi zamanı eyni vaxtda çevrilmə baş verir.

Matrislərin eşelon formasına endirilməsi

Addım matrisləri anlayışını təqdim edək: Matris var pilləli görünüş , əgər: Onda aşağıdakı ifadə doğrudur:

Əlaqədar təriflər

Elementar matris.İxtiyari B matrisini ona vurmaq B matrisində sətirlərin elementar çevrilməsinə səbəb olarsa, A matrisi elementardır.

Ədəbiyyat

İlyin V. A., Poznyak E. G. Xətti cəbr: Universitetlər üçün dərslik. - 6-cı nəşr, silinib. - M.: FİZMƏTLİT, 2004. - 280 s.

Wikimedia Fondu. 2010.

Digər lüğətlərdə "Elementar matris çevrilmələrinin" nə olduğuna baxın:

Giriş. Bu terminin dəqiq mənasında E. hissəciklər ilkin, daha da parçalana bilməyən hissəciklərdir, fərziyyə ilə bütün maddə onlardan ibarətdir. Müasirdə fizika termini "E. h." adətən tam mənasında deyil, daha az ciddi şəkildə ad üçün istifadə olunur... ... Fiziki ensiklopediya

Giriş. Bu terminin dəqiq mənasında E. hissəciklər ilkin, daha da parçalana bilməyən hissəciklərdir, fərziyyə ilə bütün maddə bunlardan ibarətdir. Konsepsiyada “E. h." müasir fizikada ibtidai varlıqlar ideyası öz ifadəsini tapır... ... Böyük Sovet Ensiklopediyası

Bu terminin başqa mənaları da var, bax Matris. Matris halqanın və ya sahənin elementlərinin düzbucaqlı cədvəli kimi yazılmış riyazi obyektdir (məsələn, tam ədədlər, reallar və ya mürəkkəb ədədlər) ... ... Vikipediya

Matris düzbucaqlı ədədlər cədvəli (və ya halqa elementləri) şəklində yazılmış və onunla digər oxşar obyektlər arasında cəbri əməliyyatlara (toplama, çıxma, vurma və s.) imkan verən riyazi obyektdir. İcra qaydaları... ... Vikipediya

Elementar çevrilmələr A matrisinin sətir və sütunlarında aşağıdakı hərəkətlərdir:

1) matrisin iki sətir və ya sütununun dəyişdirilməsi;

2) matrisin sətir və ya sütununu sıfırdan fərqli rəqəmə vurmaq;

3) bir sıraya (sütun) başqa bir sıra (sütun) əlavə etmək.

Teorem. Elementar çevrilmələr matrisin rütbəsini dəyişmir, yəni B matrisi elementar çevrilmələrlə A matrisindən alınırsa, onda.

Sübut. 1). Matrisin iki sütununu dəyişdirərkən, xətti müstəqil sütunların maksimum sayı dəyişmir və buna görə də onun dərəcəsi dəyişmir.

2). i-ci sıranı t0 və r(A) =k ədədinə vurmaqla A matrisindən B matrisi alınsın. Aydındır ki, B matrisinin i-ci cərgəsi olmayan hər hansı minoru A matrisinin müvafiq minoruna, i-ci sıranı ehtiva edən B matrisinin istənilən minoru isə A matrisinin müvafiq minorunun t ədədinə vurulmasına bərabərdir. Nəticə etibarilə, A matrisinin bazis minoruna uyğun gələn B matrisinin k dərəcəli minoru sıfırdan fərqli olacaq və B matrisinin bütün k+1 dərəcəli kiçikləri, eləcə də matrisin k+1 dərəcəli bütün minorları A, sıfıra bərabər olacaq. Bu o deməkdir ki, r(B)=k=r(A).

3). i-ci sətri j-ci sıraya əlavə etməklə A matrisindən B matrisi alınsın və r(A) = k. B matrisinin j-ci sətiri olmayan k+1 dərəcəli minorları A matrisinin müvafiq minorlarına bərabər olacaq və buna görə də sıfıra bərabər olacaqdır. I və j-ci sətirləri ehtiva edən B matrisinin k+1 dərəcəli kiçikləri iki sıfır təyinedicinin cəminə bərabər olacaqdır. Bu təyinedicilərdən biri iki eyni cərgədən ibarətdir (j-ci sətir i-ci sətirin elementlərini ehtiva edir), ikinci determinant isə A matrisinin k+1 sırasının minorudur və buna görə də sıfıra bərabərdir. B matrisinin k+1 dərəcəli kiçikləri j-ci cərgəni ehtiva edən, lakin i-ci cərgəni ehtiva etməyən A matrisinin k+1 dərəcəli iki minorunun cəminə bərabər olacaq və buna görə də ona bərabər olacaq. sıfır. Nəticə etibarı ilə B matrisinin bütün k+1 dərəcəli kiçikləri 0-a bərabərdir və r(B)k=r(A).

i sətirini (-1) vurmaqla B matrisindən C matrisi alınsın. Sonra i-ci cərgəni j-ci sıraya əlavə edib, i-ci cərgəni (-1)-ə vurmaqla C matrisindən A matrisi alınır. Deməli, yuxarıda sübut olunduğu kimi, r(A)r(C) =r(B) olacaqdır. Beləliklə, r(B)r(A) və r(A)r(B) bərabərsizlikləri eyni vaxtda etibarlıdır, bu o deməkdir ki, r(A) =r(B).

Elementar çevrilmələrin bu xassəsindən praktikada matrisin rütbəsini hesablamaq üçün istifadə olunur. Bunu etmək üçün elementar çevrilmələrdən istifadə edərək, bu (sıfırdan fərqli) A matrisini trapesiya formasına, yəni formaya endiririk.

B= ,

burada bütün i = 1,2,...,k üçün elementlər; bütün i > j üçün elementlər və

i > k. Aydındır ki, r(B) = k, yəni B matrisinin dərəcəsi sıfırdan fərqli cərgələrin sayına bərabərdir. Buradan belə çıxır ki, B matrisinin birinci k sətir və sütunların kəsişməsində yerləşən k dərəcəli minoru diaqonal təyinedicidir və ona bərabərdir; və B matrisinin k+1 tərtibli hər hansı minoru sıfır cərgədən ibarətdir, yəni 0-a bərabərdir (və ya əgər k = n olarsa, belə kiçiklər ümumiyyətlə yoxdur).

Teorem. mn ölçülü istənilən sıfırdan fərqli A matrisini elementar çevrilmələrdən istifadə etməklə trapesiya formasına endirmək olar.

Sübut. A0 olduğundan, matrisin elementi var
. Birinci və i-ci sətirləri, birinci və j-ci sütunları dəyişdirərək elementi köçürürük. matrisin yuxarı sol küncünə və işarələyin
. Sonra alınan matrisin i-ci sırasına (i= 2,3, ...,m) birinci cərgəni ədədə vururuq. . Bu elementar çevrilmələr nəticəsində matrisi əldə edirik

A
.

Əgər bütün elementlər
A matrisləri sıfıra bərabərdir, onda teorem isbat edilir. Bir element varsa
, sonra A matrisinin ikinci və i-ci sətirlərini, ikinci və j-ci sütunlarını yenidən yerləşdirərək elementi köçürürük. elementin yerinə və işarə edir
(Əgər
, sonra dərhal işarə edirik
). Sonra alınan matrisin i-ci cərgəsinə (i= 3, ...,m) ədədə vurulan ikinci cərgəni əlavə edirik. . Nəticədə matrisi alırıq

Bu prosesi davam etdirərək, sonlu sayda addımlarla B matrisini əldə edirik, yəni A matrisini trapesiya formasına endiririk.

Misal. Matrisin dərəcəsini hesablayaq



. Oklar aşağıdakı elementar çevrilmələri göstərir: 1) birinci və ikinci sətirlər dəyişdirildi; 2) dördüncü sətirə üçüncü əlavə edilsin; 3) üçüncü sətirə -2-yə vurulan birinci sətri əlavə edib, dördüncü sətri isə 3-ə bölüb; 4) üçüncü sətir 5-ə bölünərək üçüncü və dördüncü sətirlər dəyişdirildi; 5) üçüncü sətirə ikinci sətir əlavə edildi, -3-ə vuruldu, dördüncü sətirə üçüncü sətir əlavə edildi. Görünür ki, göstərilən elementar çevrilmələrlə A matrisindən alınan matris üç sıfırdan fərqli cərgə ilə trapesiya formasına malikdir. Beləliklə, r(A) = 3.

Matrisi üçbucaqlı və ya pilləli formaya endirmək üçün Qauss metodunda elementar çevrilmələrdən istifadə edilir.

Tərif

Elementar sətir çevrilmələri adlandırılır:

Bəzi xətti cəbr kurslarında matris cərgələrinin dəyişdirilməsi ayrıca elementar çevrilmə ilə ayrılmır, ona görə ki, hər hansı iki matrisin cərgəsinin dəyişməsi istənilən matrisin cərgəsini sabitə vurmaqla əldə edilə bilər. k (\displaystyle k), və matrisin hər hansı sətirinə sabitlə vurulan başqa bir sıra əlavə etmək k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

Eynilə müəyyən edilmişdir elementar sütun çevrilmələri.

Elementar çevrilmələr geri çevrilə bilən.

Qeyd matrisin olduğunu göstərir A (\displaystyle A)-dən əldə etmək olar B (\displaystyle B) elementar çevrilmələr vasitəsilə (və ya əksinə).

Xüsusiyyətlər

Elementar çevrilmələr altında invariantlığı sıralayın

Teorem (elementar çevrilmələrdə dərəcənin dəyişməzliyi haqqında).
Əgər A ∼ B (\displaystyle A\sim B), Bu r a n g A = r a n g B (\displaystyle \mathrm (zəng) A=\mathrm (zəng) B).

Elementar çevrilmələrdə SLAE-lərin ekvivalentliyi

zəng edək xətti cəbri tənliklər sistemi üzərində elementar çevrilmələr :

tənliklərin yenidən təşkili;
tənliyi sıfırdan fərqli sabitə vurmaq;
bir tənliyin digərinə əlavə edilməsi, bəzi sabitlərə vurulması.

Yəni onun genişləndirilmiş matrisi üzərində elementar çevrilmələr. Onda aşağıdakı müddəa doğrudur: Yada salaq ki, iki sistem onların həll dəstləri üst-üstə düşürsə, ekvivalent adlanır.

Tərs matrislərin tapılması

Teorem (əks matrisin tapılması haqqında).
Matrisin təyinedicisi olsun A n × n (\displaystyle A_(n\dəfə n)) sıfıra bərabər deyil, matris olsun B (\displaystyle B) ifadəsi ilə müəyyən edilir B = [ A | E ] n × 2 n (\displaystyle B=_(n\dəfə 2n)). Sonra, matrisin sıralarının elementar çevrilməsi ilə A (\displaystyle A)şəxsiyyət matrisinə E (\displaystyle E) hissəsi kimi B (\displaystyle B) transformasiya eyni vaxtda baş verir E (\displaystyle E) Kimə A − 1 (\displaystyle A^(-1)).

Kateqoriyada məşhur: