خانه › نصب و پیکربندی › چه تبدیلات ابتدایی را می توان با یک ماتریس انجام داد. جبر ماتریسی - تبدیلات اولیه ماتریس ها. ماتریس، انواع ماتریس، عملیات روی ماتریس

چه تبدیلات ابتدایی را می توان با یک ماتریس انجام داد. جبر ماتریسی - تبدیلات اولیه ماتریس ها. ماتریس، انواع ماتریس، عملیات روی ماتریس

ابتداییتبدیل رشته هاماتریس ها را تبدیل از انواع زیر می نامند:

1) ضرب هر عنصر یک رشته در همان عدد غیر صفر. رشته های باقی مانده بدون تغییر باقی می مانند (به طور خلاصه: ضرب یک رشته در یک عدد).

2) افزودن به هر عنصر از یک خط معین، عناصر مربوط به یک خط دیگر، ضرب در همان عدد. خطوط باقیمانده (شامل خطی که اضافه می شود) بدون تغییر باقی می مانند (به طور خلاصه: اضافه کردن یک خط دیگر به یک خط، ضرب در یک عدد).

3) دو ردیف از ماتریس را تعویض کنید. خطوط باقی مانده بدون تغییر باقی می مانند.

این تبدیل ها به ترتیب نامیده می شوند تحولات اولی , دومین و نوع سوم (به نوعی ). با اعمال متوالی آنها، تبدیل های پیچیده تری به دست می آوریم.

به طور مشابه تعریف شده است تبدیل ستون های ابتدایی ماتریس ها

قضیه

تبدیل نوع سوم ترکیبی از تبدیل نوع اول و دوم است.

بنابراین، تبدیل های نوع سوم را می توان به عنوان پیچیده تر از تغییرات ابتدایی طبقه بندی کرد. اما برای راحتی کار هنوز ابتدایی در نظر گرفته می شود.

قضیه

هر ماتریسی را می توان با تبدیل ردیف های ابتدایی به ماتریس پله ای کاهش داد. اگر تبدیل های ابتدایی سطرها و ستون ها را به ماتریس اعمال کنیم, سپس می توان آن را به شکل ذوزنقه ای کاهش داد.

مثلا,

á (1) خط اول و دوم را با هم عوض کنید (تبدیل نوع سوم).

(2) خط اول، ضرب در 2، به دوم اضافه شد و از سوم کم شد، در 3 ضرب شد، به چهارم اضافه شد (تبدیل نوع دوم).

(3) خط دوم از سوم و خط دوم ضرب در 14/11 از خط چهارم کم شد.

(4) خط سوم و چهارم را عوض کنید.ñ

بنابراین، ماتریس اصلی را تبدیل کردیم

به صورت مرحله ای

حال با تعویض ستون دوم و سوم و سپس تعویض آن با ستون چهارم، ستون دوم را به جای ستون چهارم منتقل می کنیم، ستون های سوم و چهارم به ترتیب در جای ستون های دوم و سوم قرار می گیرند:

بدین ترتیب ماتریس اصلی به یک ماتریس ذوزنقه ای تبدیل می شود.

تمرینات

ماتریس را به شکل پلکانی و ذوزنقه ای بیاورید:

سه عملیات بعدی نامیده می شوند تبدیل های ابتدایی ردیف های ماتریس:

1) ضرب خط i-امماتریس های عدد λ ≠ 0:

که به شکل (i) → λ(i) خواهیم نوشت.

2) جایگشت دو ردیف در یک ماتریس، به عنوان مثال ردیف های i و k ام:

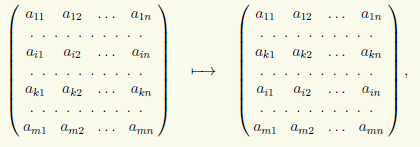
که به شکل (i) ↔ (k) خواهیم نوشت.

3) با ضریب λ به ردیف i ام ماتریس اضافه می کنیم:

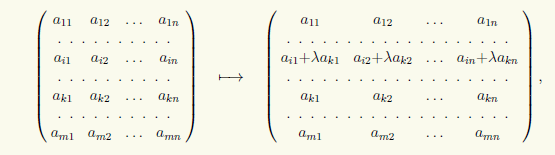
که به شکل (i) → (i) + λ(k) خواهیم نوشت.

عملیات مشابه در ستون های ماتریسی نامیده می شود تبدیل ستون های ابتدایی.

هر تبدیل ابتدایی سطرها یا ستون‌های یک ماتریس دارد تبدیل ابتدایی معکوس، که ماتریس تبدیل شده را به ماتریس اصلی تبدیل می کند. برای مثال، تبدیل معکوس برای جایگشت دو رشته، جایگشت یک رشته است.

هر تبدیل ابتدایی ردیف ها (ستون ها) ماتریس A را می توان به عنوان ضرب A در سمت چپ (راست) توسط یک ماتریس از نوع خاص تفسیر کرد. این ماتریس در صورتی به دست می آید که همان تبدیل روی آن انجام شود ماتریس هویت. بیایید نگاهی دقیق تر به تبدیل رشته های ابتدایی بیندازیم.

اجازه دهید ماتریس B نتیجه باشد ضرب i امردیف های یک ماتریس A از نوع m×n با عدد λ ≠ 0. سپس B = E i (λ)A، که در آن ماتریس E i (λ) از ماتریس هویت E از مرتبه m با ضرب i- آن به دست می آید. ردیف با عدد λ.

اجازه دهید ماتریس B در نتیجه جایگشت ردیف های i و k ام ماتریس A از نوع m×n به دست آید. سپس B = F ik A، که در آن ماتریس F ik از ماتریس هویت E از مرتبه m با جابجایی ردیف های i و k ام آن به دست می آید.

اجازه دهید ماتریس B با افزودن ردیف k ام آن با ضریب λ به ردیف i ام یک ماتریس m×n A بدست آید. سپس B = G ik (λ)Α، که در آن ماتریس G ik از ماتریس هویت E از مرتبه m با جمع کردن ردیف k با ضریب λ به ردیف i به دست می‌آید. در تقاطع ردیف i و ستون k ماتریس E، عنصر صفر با عدد λ جایگزین می شود.

تبدیل‌های اولیه ستون‌های ماتریس A دقیقاً به همان روش اجرا می‌شوند، اما در عین حال با ماتریس‌هایی از نوع خاص نه در سمت چپ، بلکه در سمت راست ضرب می‌شوند.

با استفاده از الگوریتم هایی که مبتنی بر تبدیل های ابتدایی سطرها و ستون ها هستند، ماتریس ها را می توان به انواع مختلف. یکی از مهمترین این الگوریتم ها اساس اثبات قضیه زیر را تشکیل می دهد.

قضیه 10.1.با استفاده از تبدیل های ردیف ابتدایی، هر ماتریسی را می توان به کاهش داد نمای پلکانی.

◄ اثبات قضیه عبارت است از ساختن الگوریتم خاصماتریس را به شکل مرحله ای می آورد. این الگوریتم شامل تکرار مکرر سه عملیات مرتبط با یک عنصر ماتریس فعلی است که بر اساس مکان آن در ماتریس انتخاب می شود. در مرحله اول الگوریتم، بالا سمت چپ را به عنوان عنصر فعلی ماتریس انتخاب می کنیم، یعنی. [A] 11.

1*. اگر عنصر فعلی صفر است، به عملیات 2* بروید. اگر برابر با صفر نباشد، ردیفی که عنصر جاری در آن قرار دارد (ردیف جاری) با ضرایب مناسب به ردیف های زیر اضافه می شود، به طوری که تمام عناصر ماتریس در ستون زیر عنصر فعلی صفر می شوند. به عنوان مثال، اگر عنصر فعلی [A] ij باشد، آنگاه به عنوان ضریب k-امین ردیف، k = i + 1، ...، باید عدد - [A] kj /[A] ij را بگیریم. یک عنصر فعلی جدید را انتخاب می کنیم و در ماتریس یک ستون به سمت راست و یک ردیف به پایین حرکت می کنیم و به مرحله بعد ادامه می دهیم و عملیات 1* را تکرار می کنیم. اگر چنین تغییری ممکن نباشد، یعنی. آخرین ستون یا سطر رسیده است، تغییر شکل را متوقف می کنیم.

2*. اگر عنصر فعلی در برخی از ردیف های ماتریس برابر با صفر باشد، از طریق عناصر ماتریس واقع در ستون زیر عنصر فعلی نگاه می کنیم. اگر در بین آنها غیر صفر وجود نداشته باشد به عملیات 3* اقدام می کنیم. بگذار وارد شود خط kthیک عنصر غیر صفر زیر عنصر فعلی وجود دارد. تعویض جریان و خط kthو بازگشت به عملیات 1*.

3*. اگر عنصر فعلی و همه عناصر زیر آن (در همان ستون) برابر با صفر باشند، عنصر فعلی را تغییر می دهیم و یک ستون را به سمت راست در ماتریس حرکت می دهیم. اگر چنین تغییری امکان پذیر باشد، یعنی عنصر فعلی در سمت راست ترین ستون ماتریس نباشد، عملیات 1* را تکرار می کنیم. اگر قبلاً به لبه سمت راست ماتریس رسیده باشیم و تغییر عنصر فعلی غیرممکن باشد، ماتریس یک شکل پلکانی دارد و می توانیم تبدیل را متوقف کنیم.

از آنجایی که ماتریس محدود است ابعادو در یک مرحله از الگوریتم موقعیت عنصر فعلی حداقل توسط یک ستون به سمت راست منتقل می شود، فرآیند تبدیل به پایان می رسد و در بیش از n مرحله (n تعداد ستون های ماتریس است). این بدان معنی است که لحظه ای فرا می رسد که ماتریس یک شکل پلکانی خواهد داشت.

مثال 10.10.بیایید ماتریس را تبدیل کنیم به شکل پله ای با استفاده از تبدیل رشته های ابتدایی.

با استفاده از الگوریتم حاصل از اثبات قضیه 10.1 و نوشتن ماتریس ها پس از اتمام عملیات آن، به دست می آوریم.

تبدیلات ماتریس ابتدایی- اینها تبدیلات ماتریس هستند که در نتیجه هم ارزی ماتریس ها حفظ می شود. بنابراین، تبدیل‌های ابتدایی مجموعه حل سیستم معادلات جبری خطی را که این ماتریس نشان می‌دهد، تغییر نمی‌دهد.

تبدیل های اولیه در روش گاوسی برای کاهش یک ماتریس به شکل مثلثی یا پله ای استفاده می شود.

تعریف

تبدیل رشته های ابتدایینامیده می شوند:

در برخی از دروس جبر خطی، جایگشت سطرهای ماتریس به عنوان یک تبدیل ابتدایی جداگانه متمایز نمی شود، زیرا جایگشت هر دو ردیف ماتریس را می توان با ضرب هر ردیف ماتریس در یک ثابت، و افزودن یک ردیف دیگر به هر ردیف ماتریس ضرب به دست آورد. توسط یک ثابت، .

به طور مشابه تعریف شده است تبدیل ستون های ابتدایی.

تحولات ابتدایی برگشت پذیر.

نماد نشان می دهد که ماتریس را می توان با تبدیل های ابتدایی به دست آورد (یا برعکس).

خواص

عدم تغییر رتبه تحت تبدیل های ابتدایی

معادل سازی SLAE ها تحت تبدیل های ابتدایی

بیا تماس بگیریم تبدیل های ابتدایی بر روی یک سیستم معادلات جبری خطی :

تنظیم مجدد معادلات؛
ضرب یک معادله در یک ثابت غیر صفر؛
اضافه کردن یک معادله به معادله دیگر، ضرب در مقداری ثابت.

آن ها تحولات ابتدایی بر روی ماتریس توسعه یافته آن سپس عبارت زیر درست است: به یاد بیاورید که اگر مجموعه راه حل های دو سیستم بر هم منطبق باشد، معادل نامیده می شوند.

یافتن ماتریس های معکوس

قضیه (درباره یافتن ماتریس معکوس).
اجازه دهید تعیین کننده ماتریس غیر صفر باشد، اجازه دهید ماتریس با عبارت تعریف شود. سپس، در طی یک تبدیل ابتدایی ردیف‌های ماتریس به ماتریس هویت در ترکیب، یک تبدیل به طور همزمان اتفاق می‌افتد.

کاهش ماتریس ها به شکل سطحی

اجازه دهید مفهوم ماتریس های گام را معرفی کنیم: یک ماتریس دارد نمای پلکانی , if: پس عبارت زیر درست است:

تعاریف مرتبط

ماتریس ابتداییماتریس A ابتدایی است اگر ضرب یک ماتریس دلخواه B در آن منجر به تبدیل ابتدایی ردیف های ماتریس B شود.

ادبیات

Ilyin V. A.، Poznyak E. G. جبر خطی: کتاب درسی برای دانشگاه ها. - چاپ ششم، پاک شد. - M.: FIZMATLIT، 2004. - 280 p.

بنیاد ویکی مدیا 2010.

ببینید «تبدیل‌های ماتریس ابتدایی» در فرهنگ‌های دیگر چیست:

معرفی. ه. ذرات در معنای دقیق این اصطلاح، ذرات اولیه و غیر قابل تجزیه بیشتر هستند که بر اساس فرض، تمام ماده از آنها تشکیل شده است. در مدرن اصطلاح فیزیک "E. h." معمولاً نه به معنای دقیق آن، بلکه کمتر برای نام ... ... دایره المعارف فیزیکی

معرفی. ه. ذرات در معنای دقیق این اصطلاح، ذرات اولیه و غیر قابل تجزیه بیشتر هستند که بر اساس فرض، تمام ماده از آنها تشکیل شده است. در مفهوم "E. h." در فیزیک مدرن، ایده موجودات اولیه بیان می شود... ... دایره المعارف بزرگ شوروی

این اصطلاح معانی دیگری دارد، به ماتریس مراجعه کنید. ماتریس یک شی ریاضی است که به صورت جدول مستطیلی از عناصر یک حلقه یا میدان (مثلا اعداد صحیح، واقعی یا مختلط) نوشته می شود که نشان دهنده ... ... ویکی پدیا

ماتریس یک شی ریاضی است که به شکل جدول مستطیلی از اعداد (یا عناصر یک حلقه) نوشته می شود و امکان انجام عملیات جبری (جمع، تفریق، ضرب و غیره) بین آن و سایر اشیاء مشابه را فراهم می کند. قوانین اجرا... ... ویکی پدیا

تبدیل های ابتدایی اقدامات زیر در ردیف ها و ستون های ماتریس A هستند:

1) مبادله دو سطر یا ستون از یک ماتریس؛

2) ضرب سطر یا ستون ماتریس در عددی غیر از صفر؛

3) اضافه کردن یک ردیف (ستون) دیگر به یک ردیف (ستون).

قضیه.تبدیل‌های ابتدایی رتبه ماتریس را تغییر نمی‌دهند، یعنی اگر ماتریس B از ماتریس A با تبدیل‌های ابتدایی به‌دست آید، پس.

اثبات 1). هنگام تعویض دو ستون از یک ماتریس، حداکثر تعداد ستون های مستقل خطی تغییر نمی کند و بنابراین رتبه آن تغییر نمی کند.

2). اجازه دهید ماتریس B از ماتریس A با ضرب i-امین ردیف در عدد t0 و r(A) =k بدست آید. بدیهی است که هر مینور ماتریس B که شامل ردیف i نباشد برابر با مینور مربوط به ماتریس A است و هر مینور ماتریس B حاوی ردیف i برابر است با مینور متناظر ماتریس A ضرب در عدد t. در نتیجه، مینور مرتبه k ماتریس B، مربوط به مینور پایه ماتریس A، غیر صفر خواهد بود، و همه مینورهای مرتبه k+1 ماتریس B، و همچنین همه مینورهای مرتبه k+1 ماتریس، غیرصفر خواهند بود. A برابر با صفر خواهد بود. یعنی r(B)=k=r(A).

3). اجازه دهید ماتریس B از ماتریس A با افزودن ردیف i به ردیف j و r(A) = k بدست آید. مینورهای مرتبه k+1 ماتریس B که دارای ردیف j نیستند برابر با مینورهای مربوط به ماتریس A و در نتیجه برابر با صفر خواهند بود. مینورهای مرتبه k+1 ماتریس B حاوی ردیف ith و j ام برابر با مجموع دو تعیین کننده صفر خواهند بود. یکی از این تعیین کننده ها شامل دو ردیف یکسان است (ردیف j ام شامل عناصر ردیف i است) و تعیین کننده دوم جزئی از مرتبه k+1 ماتریس A است و بنابراین برابر با صفر است. مینورهای مرتبه k+1 ماتریس B، حاوی ردیف j، اما فاقد ردیف i، برابر با مجموع دو مینور از مرتبه k+1 ماتریس A خواهد بود و بنابراین نیز برابر با صفر در نتیجه، تمام مینورهای مرتبه k+1 ماتریس B برابر با 0 و r(B)k=r(A) هستند.

اجازه دهید ماتریس C از ماتریس B با ضرب ردیف i در (-1) بدست آید. سپس ماتریس A از ماتریس C با افزودن ردیف i به ردیف j و ضرب ردیف i در (-1) به دست می آید. بنابراین، همانطور که در بالا ثابت شد، r(A)r(C) =r(B) وجود خواهد داشت. بنابراین، نابرابری های r(B)r(A) و r(A)r(B) به طور همزمان معتبر هستند، به این معنی که r(A) =r(B).

این ویژگی تبدیل های ابتدایی در عمل برای محاسبه رتبه یک ماتریس استفاده می شود. برای انجام این کار، با استفاده از تبدیل های ابتدایی، ماتریس A (غیر صفر) را به شکل ذوزنقه ای، یعنی به شکل، کاهش می دهیم.

B= ,

که در آن عناصر برای همه i = 1,2,...,k; عناصر برای همه i > j و

i > k. بدیهی است r(B) = k، یعنی رتبه ماتریس B برابر است با تعداد ردیف های غیر صفر. این از این واقعیت ناشی می شود که جزئی مرتبه k ماتریس B که در تقاطع اولین k ردیف و ستون قرار دارد، یک تعیین کننده مورب است و برابر است با. و هر مینور از مرتبه k+1 ماتریس B حاوی یک ردیف صفر است، به این معنی که برابر 0 است (یا اگر k = n، اصلاً چنین مینورهایی وجود ندارد).

قضیه.هر ماتریس غیر صفر A با بعد mn را می توان با استفاده از تبدیل های ابتدایی به شکل ذوزنقه ای کاهش داد.

اثباتاز آنجایی که A0، یک عنصر ماتریسی وجود دارد
. با تعویض ردیف های اول و iام، ستون های اول و j ام، عنصر را جابه جا می کنیم. به گوشه سمت چپ بالای ماتریس بروید و نشان دهید
. سپس به ردیف i-ام ماتریس حاصل (i= 2,3, ...,m) اولین ردیف ضرب در عدد را اضافه می کنیم. . در نتیجه این تبدیل های ابتدایی، ماتریس را به دست می آوریم

آ
.

اگر همه عناصر
ماتریس های A برابر با صفر هستند، سپس قضیه ثابت می شود. اگر عنصری وجود دارد
، سپس با مرتب کردن مجدد ردیف های دوم و iام، ستون های دوم و j ام ماتریس A، عنصر را جابجا می کنیم. به جای عنصر و نشان دهند
(اگر
، سپس بلافاصله نشان می دهیم
). سپس به ردیف i-امین ماتریس حاصل (i= 3, ...,m) ردیف دوم ضرب در عدد را اضافه می کنیم. . در نتیجه ماتریس را بدست می آوریم

در ادامه این فرآیند، در تعداد محدودی از مراحل، ماتریس B را به دست می آوریم، یعنی ماتریس A را به شکل ذوزنقه ای کاهش می دهیم.

مثال.بیایید رتبه ماتریس را محاسبه کنیم



. فلش ها تبدیل های اولیه زیر را نشان می دهند: 1) خطوط اول و دوم تعویض شدند. 2) یک سوم به خط چهارم اضافه شد. 3) خط اول را با ضرب در 2- به خط سوم اضافه کرد و خط چهارم را بر 3 تقسیم کرد. 4) خط سوم را بر 5 تقسیم کرد و خط سوم و چهارم را عوض کرد. 5) یک خط دوم به خط سوم اضافه شد که در -3 ضرب شد و یک سوم به خط چهارم اضافه شد. مشاهده می شود که ماتریس به دست آمده از ماتریس A با تبدیل های ابتدایی نشان داده شده دارای شکل ذوزنقه ای با سه ردیف غیر صفر است. بنابراین r(A) = 3.

تبدیل های اولیه در روش گاوسی برای کاهش یک ماتریس به شکل مثلثی یا پله ای استفاده می شود.

تعریف

تبدیل رشته های ابتدایینامیده می شوند:

در برخی درس‌های جبر خطی، جایگشت ردیف‌های ماتریس به یک تبدیل ابتدایی جداگانه تفکیک نمی‌شود، زیرا جایگشت هر دو ردیف ماتریسی را می‌توان با ضرب هر ردیف ماتریسی در یک ثابت به دست آورد. k (\displaystyle k)، و به هر ردیفی از ماتریس یک ردیف دیگر اضافه می کنیم که در یک ثابت ضرب می شود k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

به طور مشابه تعریف شده است تبدیل ستون های ابتدایی.

تحولات ابتدایی برگشت پذیر.

نماد نشان می دهد که ماتریس A (\displaystyle A)را می توان از B (\displaystyle B)از طریق دگرگونی های ابتدایی (یا برعکس).

خواص

عدم تغییر رتبه تحت تبدیل های ابتدایی

قضیه (در مورد تغییر ناپذیری رتبه تحت تبدیل های ابتدایی).
اگر A ~ B (\displaystyle A\sim B)، آن r a n g A = r a n g B (\displaystyle \mathrm (رنگ) A=\mathrm (رنگ) B).

معادل سازی SLAE ها تحت تبدیل های ابتدایی

بیا تماس بگیریم تبدیل های ابتدایی بر روی یک سیستم معادلات جبری خطی :

تنظیم مجدد معادلات؛
ضرب یک معادله در یک ثابت غیر صفر؛
اضافه کردن یک معادله به معادله دیگر، ضرب در مقداری ثابت.

یعنی تحولات ابتدایی بر روی ماتریس بسط یافته آن. سپس عبارت زیر درست است: به یاد بیاورید که اگر مجموعه راه حل های دو سیستم بر هم منطبق باشد، معادل نامیده می شوند.

یافتن ماتریس های معکوس

قضیه (درباره یافتن ماتریس معکوس).
اجازه دهید تعیین کننده ماتریس A n × n (\displaystyle A_(n\times n))برابر با صفر نیست، اجازه دهید ماتریس B (\displaystyle B)با بیان مشخص می شود B = [ A | E ] n × 2 n (\displaystyle B=_(n\times 2n)). سپس، با یک تبدیل ابتدایی ردیف های ماتریس A (\displaystyle A)به ماتریس هویت E (\displaystyle E)بعنوان بخشی از B (\displaystyle B)دگرگونی در همان زمان رخ می دهد E (\displaystyle E)به A − 1 (\displaystyle A^(-1)).

محبوب در دسته بندی: