Milyen elemi transzformációk végezhetők mátrixszal. Mátrix algebra - mátrixok elemi transzformációi. Mátrix, mátrixok típusai, műveletek mátrixokon

Alapvetőkarakterlánc konverziók A mátrixokat a következő típusú transzformációknak nevezzük:

1) Egy karakterlánc minden elemének megszorzása ugyanazzal a nullától eltérő számmal. A fennmaradó karakterláncok változatlanok maradnak (röviden: egy karakterláncot megszorozunk egy számmal).

2) Egy bizonyos sor minden eleméhez hozzáadjuk egy másik sor megfelelő elemeit, megszorozva ugyanazzal a számmal. A fennmaradó sorok (beleértve a hozzáadott sorokat is) változatlanok maradnak (röviden: újabb sor hozzáadása egy sorhoz, megszorozva egy számmal).

3) Cserélje fel a mátrix két sorát. A többi sor változatlan marad.

Ezeket a transzformációkat ill az első átalakulásai , második És harmadik típus (fajta ). Ezeket szekvenciálisan alkalmazva összetettebb transzformációkat kapunk.

Hasonlóan meghatározott elemi oszloptranszformációk mátrixok.

Tétel

A harmadik típusú transzformáció az első és a második típusú transzformációk valamilyen kombinációja.

Így a harmadik típusú transzformációk összetettebbek, mint az elemiek. De a kényelem kedvéért még mindig eleminek számít.

Tétel

Bármely mátrix redukálható lépésmátrixsá elemi sortranszformációkkal. Ha sorok és oszlopok elemi transzformációit alkalmazzuk a mátrixra, akkor trapéz alakúra redukálható.

Például,

á(1) Cserélje fel az első és a második sort (a harmadik típusú transzformáció).

(2) Az első sort 2-vel szorozva hozzáadtuk a másodikhoz, és kivontuk a harmadikból, megszoroztuk 3-mal, hozzáadtuk a negyedikhez (második típusú transzformációk).

(3) A második sort a harmadikból, a második sort pedig 14/11-gyel szorozva a negyedikből kivontuk.

(4) Cserélje fel a harmadik és a negyedik sort.ñ

Így az eredeti mátrixot átalakítottuk

lépésenkénti módon

Most, miután felcseréltük a második és harmadik oszlopot, majd felcseréltük a negyedik oszlopra, áthelyezzük a második oszlopot a negyedik helyére, a harmadik és a negyedik oszlop a második és harmadik oszlop helyén jelenik meg:

ezáltal az eredeti mátrixot trapéz alakúvá alakítja át.

Feladatok

Hozd a mátrixot lépcsős és trapéz alakúra:

A következő három műveletet hívjuk mátrixsorok elemi transzformációi:

1) Szorzás i-edik sor mátrixok a λ ≠ 0 számhoz:

amelyet az (i) → λ(i) alakban fogunk írni.

2) Két sor permutációja egy mátrixban, például az i-edik és a k-adik sor:

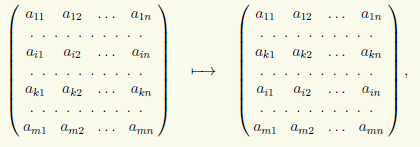
amelyet (i) ↔ (k) formában fogunk írni.

3) A mátrix i-edik sorához hozzáadjuk a λ együtthatójú k-adik sorát:

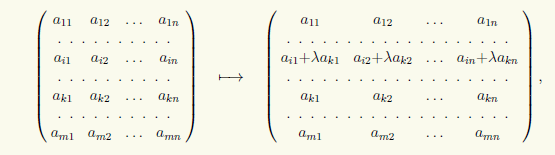
amelyet (i) → (i) + λ(k) formában fogunk felírni.

A mátrixoszlopokon végzett hasonló műveleteket nevezzük elemi oszloptranszformációk.

A mátrix sorainak vagy oszlopainak minden elemi transzformációja rendelkezik inverz elemi transzformáció, amely a transzformált mátrixot eredetivé alakítja. Például két karakterlánc permutálására szolgáló inverz transzformáció ugyanazon karakterláncok permutációja.

Az A mátrix sorainak (oszlopainak) minden elemi transzformációja a bal (jobb) A szorzataként értelmezhető egy speciális típusú mátrixszal. Ezt a mátrixot akkor kapjuk meg, ha ugyanazt a transzformációt hajtjuk végre identitásmátrix. Nézzük meg közelebbről az elemi karakterlánc-konverziókat.

Legyen B mátrix az eredmény i-edik szorzás egy m×n típusú A mátrix sorai a λ ≠ 0 számmal. Ekkor B = E i (λ)A, ahol az E i (λ) mátrixot az m rendű E identitásmátrixból kapjuk úgy, hogy megszorozzuk annak i- sorban a λ számmal.

Legyen a B mátrix az A mátrix m×n típusú i-edik és k-edik sorának permutációja eredményeként. Ekkor B = F ik A, ahol az F ik mátrixot az m rendű E azonosságmátrixból kapjuk, annak i-edik és k-edik sorát átrendezve.

Kapjuk meg a B mátrixot úgy, hogy egy m×n A mátrix i-edik sorához adjuk a λ együtthatós k-edik sorát. Ekkor B = G ik (λ)А, ahol a G ik mátrixot az m rendű E azonosságmátrixból kapjuk úgy, hogy az i-edik sorhoz hozzáadjuk a λ együtthatójú k-edik sort, azaz. az E mátrix i-edik sorának és k-adik oszlopának metszéspontjában a nulla elemet a λ számmal helyettesítjük.

Az A mátrix oszlopainak elemi transzformációi pontosan ugyanígy valósulnak meg, ugyanakkor nem bal, hanem jobb oldali speciális típusú mátrixokkal szorozzuk meg.

Sorok és oszlopok elemi átalakításán alapuló algoritmusok segítségével a mátrixok átalakíthatók különféle típusok. Az egyik legfontosabb ilyen algoritmus képezi a következő tétel bizonyításának alapját.

10.1. Tétel. Elemi sortranszformációk segítségével bármilyen mátrixra redukálható lépcsős nézet.

◄ A tétel bizonyítása a konstrukcióból áll konkrét algoritmus a mátrix lépésenkénti formába hozása. Ez az algoritmus abból áll, hogy bizonyos sorrendben ismételten megismétlünk három műveletet, amelyek valamilyen aktuális mátrixelemhez kapcsolódnak, és amely a mátrixban elfoglalt helye alapján kerül kiválasztásra. Az algoritmus első lépésében a bal felsőt választjuk ki a mátrix aktuális elemének, azaz. [A] 11 .

1*. Ha az aktuális elem nulla, lépjen a 2* műveletre. Ha nem egyenlő nullával, akkor azt a sort, amelyben az aktuális elem található (az aktuális sort), a megfelelő együtthatókkal hozzáadjuk az alatta lévő sorokhoz, így az aktuális elem alatti oszlopban az összes mátrixelem nullává válik. Például, ha az aktuális elem [A] ij , akkor a k-edik sor együtthatójaként, k = i + 1, ... , a - [A] kj /[A] ij számot kell vennünk. Kijelölünk egy új aktuális elemet, a mátrixban egy oszloppal jobbra és egy sorral lefelé haladva, és továbblépünk a következő lépésre, megismételve az 1* műveletet. Ha ilyen váltás nem lehetséges, pl. az utolsó oszlopot vagy sort elértük, leállítjuk az átalakítást.

2*. Ha a mátrix valamelyik sorában az aktuális elem nullával egyenlő, akkor átnézzük az aktuális elem alatti oszlopban található mátrixelemeket. Ha nincs köztük nullától eltérő egy, akkor folytatjuk a 3* műveletet. Beengedni k-edik sor az aktuális elem alatt van egy nem nulla elem. Cserélje ki az aktuális és k-edik sorés térjen vissza az 1* művelethez.

3*. Ha az aktuális elem és az alatta lévő összes elem (ugyanabban az oszlopban) nulla, akkor megváltoztatjuk az aktuális elemet, egy oszlopot jobbra mozgatva a mátrixban. Ha lehetséges ilyen eltolás, azaz az aktuális elem nincs a mátrix jobb szélső oszlopában, akkor megismételjük az 1* műveletet. Ha már elértük a mátrix jobb szélét, és az aktuális elem megváltoztatása lehetetlen, akkor a mátrixnak lépcsőzetes formája van, és abbahagyhatjuk a transzformációt.

Mivel a mátrixnak véges méretek, és az algoritmus egyik lépésében az aktuális elem pozícióját legalább egy oszloppal jobbra toljuk, a transzformációs folyamat véget ér, és legfeljebb n lépésben (n a mátrix oszlopainak száma). Ez azt jelenti, hogy eljön az a pillanat, amikor a mátrixnak lépcsőzetes formája lesz.

10.10. példa. Alakítsuk át a mátrixot elemi karakterlánc-transzformációk segítségével lépcsőzetes formába hozni.

A 10.1. Tétel bizonyításának algoritmusát felhasználva és a mátrixokat a műveletek befejezése után felírva kapjuk

Elemi mátrix transzformációk- ezek a mátrix transzformációi, amelyek eredményeként a mátrixok ekvivalenciája megmarad. Így az elemi transzformációk nem változtatják meg a mátrix által képviselt lineáris algebrai egyenletrendszer megoldáskészletét.

A Gauss-módszerben elemi transzformációkat használnak a mátrix háromszög vagy lépcsős formára való redukálására.

Meghatározás

Elemi karakterlánc-konverziók hívják:

Egyes lineáris algebrai kurzusokban a mátrixsorok permutációját nem különböztetjük meg külön elemi transzformációként, mivel bármely két mátrixsor permutációját megkaphatjuk úgy, hogy bármely mátrixsort megszorozunk egy konstanssal, és bármely mátrixsorhoz hozzáadunk egy másik sort. állandóval , .

Hasonlóan meghatározott elemi oszloptranszformációk.

Elemi átalakulások megfordítható.

A jelölés azt jelzi, hogy a mátrix elemi transzformációkkal nyerhető (vagy fordítva).

Tulajdonságok

Rang invariancia elemi transzformációk alatt

SLAE-ek ekvivalenciája elemi transzformációk alatt

Hívjuk fel elemi transzformációk lineáris algebrai egyenletrendszeren :

• egyenletek átrendezése;
• egy egyenletet megszorozunk egy nem nulla állandóval;
• az egyik egyenlet hozzáadása a másikhoz, megszorozva valamilyen konstanssal.

Azok. elemi transzformációkat a kiterjesztett mátrixán. Ekkor igaz a következő állítás: Emlékezzünk vissza, hogy két rendszert ekvivalensnek nevezünk, ha a megoldáshalmazaik egybeesnek.

Inverz mátrixok keresése

Tétel (az inverz mátrix megtalálásáról). Legyen a mátrix determinánsa nullától eltérő, a mátrixot a kifejezés határozza meg. Ezután a mátrix sorainak elemi transzformációja során a kompozícióban lévő identitásmátrixsá egyidejűleg egy transzformáció következik be.

Mátrixok redukálása lépcsőzetes formára

Vezessük be a lépésmátrixok fogalmát: A mátrixnak van lépcsős nézet , ha: Akkor igaz a következő állítás:

Kapcsolódó definíciók

Elemi mátrix. Az A mátrix elemi, ha egy tetszőleges B mátrixot megszorozunk vele, a B mátrix sorainak elemi transzformációjához vezet.

Irodalom

Iljin V. A., Poznyak E. G. Lineáris algebra: Tankönyv egyetemek számára. - 6. kiadás, törölve. - M.: FIZMATLIT, 2004. - 280 p.

Wikimédia Alapítvány. 2010.

Nézze meg, mik az „elemi mátrix transzformációk” más szótárakban:

Bevezetés. Az E. részecskék e kifejezés pontos értelmében elsődleges, tovább bomlhatatlan részecskék, amelyekből feltételezés szerint minden anyag áll. Modernben fizika kifejezés "E. h." általában nem a pontos jelentésében, hanem kevésbé szigorúan a névre használják... ... Fizikai enciklopédia

Bevezetés. Az E. részecskék e kifejezés pontos értelmében elsődleges, tovább bomlhatatlan részecskék, amelyekből feltételezés szerint minden anyag áll. Az „E. h." a modern fizikában az őslények gondolata kifejezésre jut... ... Nagy szovjet enciklopédia

Ennek a kifejezésnek más jelentése is van, lásd a Mátrixot. A mátrix egy matematikai objektum, amely egy gyűrű vagy mező elemeinek téglalap alakú táblázataként van megírva (például egész számok, valós számok vagy komplex számok), amely ... ... Wikipédia

A mátrix egy matematikai objektum, amely négyszögletes számtáblázat (vagy egy gyűrű elemei) formájában van írva, és lehetővé teszi az algebrai műveleteket (összeadás, kivonás, szorzás stb.) közte és más hasonló objektumok között. A végrehajtás szabályai... ... Wikipédia

A mátrix egy matematikai objektum, amely négyszögletes számtáblázat (vagy egy gyűrű elemei) formájában van írva, és lehetővé teszi az algebrai műveleteket (összeadás, kivonás, szorzás stb.) közte és más hasonló objektumok között. A végrehajtás szabályai... ... Wikipédia

A mátrix egy matematikai objektum, amely négyszögletes számtáblázat (vagy egy gyűrű elemei) formájában van írva, és lehetővé teszi az algebrai műveleteket (összeadás, kivonás, szorzás stb.) közte és más hasonló objektumok között. A végrehajtás szabályai... ... Wikipédia

A mátrix egy matematikai objektum, amely négyszögletes számtáblázat (vagy egy gyűrű elemei) formájában van írva, és lehetővé teszi az algebrai műveleteket (összeadás, kivonás, szorzás stb.) közte és más hasonló objektumok között. A végrehajtás szabályai... ... Wikipédia

A mátrix egy matematikai objektum, amely négyszögletes számtáblázat (vagy egy gyűrű elemei) formájában van írva, és lehetővé teszi az algebrai műveleteket (összeadás, kivonás, szorzás stb.) közte és más hasonló objektumok között. A végrehajtás szabályai... ... Wikipédia

Az elemi transzformációk a következő műveletek az A mátrix sorain és oszlopain:

1) mátrix két sorának vagy oszlopának felcserélése;

2) mátrix egy sorának vagy oszlopának szorzása nullától eltérő számmal;

3) újabb sor (oszlop) hozzáadása egy sorhoz (oszlophoz).

Tétel. Az elemi transzformációk nem változtatják meg a mátrix rangját, vagyis ha B mátrixot elemi transzformációkkal kapunk az A mátrixból, akkor.

Bizonyíték. 1). Egy mátrix két oszlopának felcserélésekor a lineárisan független oszlopok maximális száma nem változik, így a rangja sem.

2). Legyen a B mátrix az A mátrixból úgy, hogy az i-edik sort megszorozzuk a t0 számmal és r(A) =k. Nyilvánvaló, hogy a B mátrix bármely mollja, amely nem tartalmazza az i-edik sort, egyenlő az A mátrix megfelelő molljával, és a B mátrix bármely, az i-edik sort tartalmazó mollja egyenlő az A mátrix megfelelő molljával, szorozva t számmal. Következésképpen a B mátrix k rendű mollja, amely az A mátrix alapmolljának felel meg, nullától eltérő lesz, és a B mátrix összes k+1 rendű mollja, valamint a mátrix összes k+1 rendű mollja. A, egyenlő lesz nullával. Ez azt jelenti, hogy r(B)=k=r(A).

3). Legyen B mátrix az A mátrixból úgy, hogy az i-edik sort hozzáadjuk a j-edikhez, és r(A) = k. A B mátrix k+1 rendű minorjai, amelyek nem tartalmazzák a j-edik sort, egyenlők lesznek az A mátrix megfelelő minorjaival, ezért egyenlők nullával. A B mátrix i-edik és j-edik sorát tartalmazó k+1 rendű minorjai egyenlők két nulla determináns összegével. Az egyik ilyen determináns két egyforma sort tartalmaz (a j-edik sor az i-edik sor elemeit tartalmazza), a második determináns pedig az A mátrix k+1 rendű mollja, ezért egyenlő nullával. A B mátrix k+1 rendű, a j-edik sorát tartalmazó, de az i-edik sort nem tartalmazó minorjai egyenlők lesznek az A mátrix két k+1-es rendű molljának összegével, ezért egyenlők lesznek nulla. Következésképpen a B mátrix minden k+1 rendű minora egyenlő 0-val, és r(B)k=r(A).

Legyen a C mátrix a B mátrixból úgy, hogy az i sort megszorozzuk (-1)-gyel. Ekkor az A mátrixot a C mátrixból úgy kapjuk meg, hogy az i-edik sort a j-edik sorhoz adjuk, és az i-edik sort megszorozzuk (-1-gyel). Ezért, ahogy fentebb bebizonyosodott, r(A)r(C) =r(B) lesz. Így az r(B)r(A) és r(A)r(B) egyenlőtlenségek egyidejűleg érvényesek, ami azt jelenti, hogy r(A) =r(B).

Az elemi transzformációknak ezt a tulajdonságát a gyakorlatban egy mátrix rangjának kiszámítására használják. Ehhez elemi transzformációk segítségével ezt a (nem nulla) A mátrixot trapéz alakúra, azaz alakra redukáljuk.

B= ,

ahol az összes i elem = 1,2,...,k; elemek minden i > j és

i > k. Nyilvánvalóan r(B) = k, vagyis a B mátrix rangja megegyezik a nullától eltérő sorok számával. Ez abból a tényből következik, hogy a B mátrix k rendű mollja, amely az első k sor és oszlop metszéspontjában található, átlós determináns, és egyenlő; és a B mátrix bármely k+1 rendű mollja nulla sort tartalmaz, ami azt jelenti, hogy egyenlő 0-val (vagy ha k = n, akkor egyáltalán nincsenek ilyen mollok).

Tétel. Bármely mn méretű nem nulla A mátrix trapéz alakúra redukálható elemi transzformációkkal.

Bizonyíték. Mivel A0, akkor van mátrixelem
. Az első és az i-edik sor, az első és a j-edik oszlop felcserélésével mozgatjuk az elemet a mátrix bal felső sarkába, és jelölje
. Ezután a kapott mátrix i-edik sorába (i= 2,3, ...,m) hozzáadjuk az első sort a számmal szorozva . Ezen elemi transzformációk eredményeként megkapjuk a mátrixot

A
.

Ha minden elem
Az A mátrixok nullával egyenlőek, akkor a tétel bizonyítást nyer. Ha van olyan elem
, akkor az A mátrix második és i-edik sorát, második és j-edik oszlopát átrendezve mozgatjuk az elemet az elem helyére és jelöljük
(Ha
, akkor azonnal jelöljük
). Ezután a kapott mátrix i-edik sorához (i= 3, ...,m) hozzáadjuk a második sort a számmal szorozva . Ennek eredményeként megkapjuk a mátrixot

.

Ezt a folyamatot folytatva véges számú lépésben megkapjuk a B mátrixot, vagyis az A mátrixot trapéz alakúra redukáljuk.

Példa. Számítsuk ki a mátrix rangját!



. A nyilak a következő elemi transzformációkat jelzik: 1) az első és a második sor felcserélődött; 2) hozzáadott egy harmadikat a negyedik sorhoz; 3) hozzáadta az első sort -2-vel megszorozva a harmadik sorhoz, és elosztotta a negyedik sort 3-mal; 4) elosztotta a harmadik sort 5-tel, és felcserélte a harmadik és negyedik sort; 5) egy második sort adtunk a harmadik sorhoz, megszorozva -3-mal, és egy harmadikat a negyedik sorhoz. Látható, hogy az A mátrixból a jelzett elemi transzformációkkal kapott mátrix trapéz alakú, három nem nulla sorral. Ezért r(A) = 3.

Elemi mátrix transzformációk- ezek a mátrix transzformációi, amelyek eredményeként a mátrixok ekvivalenciája megmarad. Így az elemi transzformációk nem változtatják meg a mátrix által képviselt lineáris algebrai egyenletrendszer megoldáskészletét.

A Gauss-módszerben elemi transzformációkat használnak a mátrix háromszög vagy lépcsős formára való redukálására.

Meghatározás

Elemi karakterlánc-konverziók hívják:

Egyes lineáris algebrai kurzusokban a mátrixsorok permutációját nem különítik el külön elemi transzformációba, mivel bármely két mátrixsor permutációja elérhető bármely mátrixsor konstans szorzásával. k (\displaystyle k), és a mátrix bármely sorához hozzáadunk egy újabb sort, megszorozva egy konstanssal k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

Hasonlóan meghatározott elemi oszloptranszformációk.

Elemi átalakulások megfordítható.

A jelölés azt jelzi, hogy a mátrix A (\displaystyle A) től szerezhető be B (\megjelenítési stílus B) elemi transzformációk révén (vagy fordítva).

Tulajdonságok

Rang invariancia elemi transzformációk alatt

Tétel (a rang invarianciájáról elemi transzformációknál). Ha A ~ B (\displaystyle A\sim B), Azt r a n g A = r a n g B (\displaystyle \mathrm (cseng) A=\mathrm (cseng) B).

SLAE-ek ekvivalenciája elemi transzformációk alatt

Hívjuk fel elemi transzformációk lineáris algebrai egyenletrendszeren :

• egyenletek átrendezése;
• egy egyenletet megszorozunk egy nem nulla állandóval;
• az egyik egyenlet hozzáadása a másikhoz, megszorozva valamilyen konstanssal.

Azaz elemi transzformációk a kiterjesztett mátrixán. Ekkor igaz a következő állítás: Emlékezzünk vissza, hogy két rendszert ekvivalensnek nevezünk, ha a megoldáshalmazaik egybeesnek.

Inverz mátrixok keresése

Tétel (az inverz mátrix megtalálásáról). Legyen a mátrix determinánsa A n × n (\displaystyle A_(n\times n)) nem egyenlő nullával, legyen a mátrix B (\megjelenítési stílus B) kifejezés határozza meg B = [ A | E ] n × 2 n (\displaystyle B=_(n\times 2n)). Ezután a mátrix sorok elemi transzformációjával A (\displaystyle A) az identitásmátrixhoz E (\displaystyle E) részeként B (\megjelenítési stílus B) az átalakulás egyszerre történik E (\displaystyle E) Nak nek A − 1 (\displaystyle A^(-1)).