Ce transformări elementare pot fi efectuate cu o matrice. Algebra matriceală - transformări elementare ale matricelor. Matrice, tipuri de matrice, operații pe matrice

Elementarconversii de șiruri matricele se numesc transformări de următoarele tipuri:

1) Înmulțirea fiecărui element al unui șir cu același număr diferit de zero. Șirurile rămase rămân neschimbate (pe scurt: înmulțirea unui șir cu un număr).

2) Adăugarea fiecărui element dintr-o anumită linie a elementelor corespunzătoare unei alte linii, înmulțite cu același număr. Liniile rămase (inclusiv cea adăugată) rămân neschimbate (pe scurt: adăugarea unei alte linii la o linie, înmulțită cu un număr).

3) Schimbați două rânduri ale matricei. Rândurile rămase rămân neschimbate.

Aceste transformări se numesc respectiv transformări ale primului , al doilea Și al treilea tip (un fel de ). Aplicându-le secvenţial, obţinem transformări mai complexe.

Definit în mod similar transformări elementare ale coloanei matrici.

Teorema

O transformare de al treilea tip este o combinație de transformări ale primului și al doilea tip.

Astfel, transformările de al treilea tip pot fi clasificate ca fiind mai complexe decât cele elementare. Dar este încă considerat elementar din motive de comoditate.

Teorema

Orice matrice poate fi redusă la o matrice în trepte prin transformări elementare de rând. Dacă aplicăm matricei transformări elementare de rânduri și coloane, apoi poate fi redusă la o formă trapezoidală.

De exemplu,

á(1) Schimbați prima și a doua linie (transformarea celui de-al treilea tip).

(2) Prima linie, înmulțită cu 2, a fost adăugată la a doua și s-a scăzut din a treia, înmulțită cu 3, adăugată la a patra (transformări de al doilea tip).

(3) A doua linie a fost scăzută din a treia și a doua linie înmulțită cu 14/11 a fost scăzută din a patra.

(4) Schimbați a treia și a patra linie.ñ

Astfel, am transformat matricea originală

în mod treptat

Acum, după ce am schimbat a doua și a treia coloană, apoi am schimbat-o cu a patra coloană, mutăm a doua coloană în locul celei de-a patra, a treia și a patra coloană vor fi în locul celei de-a doua și, respectiv, a treia coloană:

transformând astfel matricea originală într-una trapezoidală.

Exerciții

Aduceți matricea în forme trepte și trapezoidale:

Următoarele trei operații sunt numite transformări elementare ale rândurilor matriceale:

1) Înmulțirea I-a linie matrici pentru numărul λ ≠ 0:

pe care o vom scrie sub forma (i) → λ(i).

2) Permutarea a două rânduri dintr-o matrice, de exemplu rândurile i-lea și k-lea:

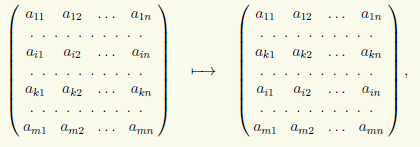
pe care o vom scrie sub forma (i) ↔ (k).

3) Adăugând la al-lea rând al matricei k-lea rând cu coeficientul λ:

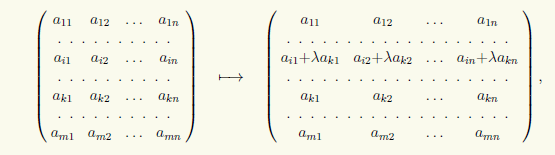
pe care o vom scrie sub forma (i) → (i) + λ(k).

Operații similare pe coloanele matrice sunt numite transformări elementare ale coloanei.

Fiecare transformare elementară a rândurilor sau coloanelor unei matrice are transformare elementară inversă, care transformă matricea transformată în cea originală. De exemplu, transformarea inversă pentru permutarea a două șiruri este de a permuta aceleași șiruri.

Fiecare transformare elementară a rândurilor (coloanelor) matricei A poate fi interpretată ca o înmulțire a lui A din stânga (dreapta) cu o matrice de formă specială. Această matrice se obține dacă se efectuează aceeași transformare matrice de identitate. Să aruncăm o privire mai atentă asupra conversiilor elementare de șiruri.

Fie matricea B rezultatul i-a înmulțire rânduri ale unei matrice A de tip m×n cu numărul λ ≠ 0. Atunci B = E i (λ)A, unde matricea E i (λ) se obține din matricea de identitate E de ordinul m prin înmulțirea lui i- al-lea rând după numărul λ.

Fie obținută matricea B ca rezultat al permutării rândurilor i și k ale matricei A de tip m×n. Atunci B = F ik A, unde matricea F ik se obține din matricea de identitate E de ordinul m prin permutarea rândurilor sale i-lea și k-lea.

Fie ca matricea B să fie obținută prin adăugarea rândului său k cu coeficientul λ la rândul i al unei matrice m×n A. Atunci B = G ik (λ)А, unde matricea G ik se obține din matricea de identitate E de ordinul m prin adăugarea rândului k cu coeficientul λ la rândul i, adică. la intersecția rândului i și coloanei k a matricei E, elementul zero este înlocuit cu numărul λ.

Transformările elementare ale coloanelor matricei A sunt implementate exact în același mod, dar în același timp este înmulțită cu matrici de tip special nu în stânga, ci în dreapta.

Folosind algoritmi care se bazează pe transformări elementare de rânduri și coloane, matricele pot fi transformate în tipuri variate. Unul dintre cei mai importanți astfel de algoritmi stă la baza demonstrației următoarei teoreme.

Teorema 10.1. Folosind transformări elementare de rând, orice matrice poate fi redusă la vedere în trepte.

◄ Demonstrarea teoremei constă în construirea algoritm specific aducând matricea într-o formă treptată. Acest algoritm constă în repetarea în mod repetat, într-o anumită ordine, a trei operații asociate cu un element de matrice curent, care este selectat în funcție de locația sa în matrice. La primul pas al algoritmului, îl selectăm pe cel din stânga sus ca element curent al matricei, adică. [A] 11 .

1*. Dacă elementul curent este zero, treceți la operația 2*. Dacă nu este egal cu zero, atunci rândul în care se află elementul curent (rândul curent) se adaugă cu coeficienții corespunzători la rândurile situate mai jos, astfel încât toate elementele matricei din coloana de sub elementul curent să devină zero. De exemplu, dacă elementul curent este [A] ij , atunci ca coeficient pentru al-lea rând, k = i + 1, ... , ar trebui să luăm numărul - [A] kj /[A] ij . Selectăm un nou element curent, deplasându-ne în matrice o coloană la dreapta și un rând în jos și trecem la pasul următor, repetând operația 1*. Dacă o astfel de schimbare nu este posibilă, de ex. s-a ajuns la ultima coloană sau rând, oprim transformarea.

2*. Dacă elementul curent dintr-un rând al matricei este egal cu zero, atunci ne uităm prin elementele matricei situate în coloana de sub elementul curent. Dacă printre ele nu există altele diferite de zero, trecem la operația 3*. Lăsa să intre a k-a linie există un element diferit de zero sub elementul curent. Schimbați curentul și a k-a linieși reveniți la operațiunea 1*.

3*. Dacă elementul curent și toate elementele de sub el (în aceeași coloană) sunt egale cu zero, schimbăm elementul curent, deplasând o coloană la dreapta în matrice. Dacă o astfel de schimbare este posibilă, adică elementul curent nu se află în coloana din dreapta a matricei, atunci repetăm ​​operația 1*. Dacă am ajuns deja la marginea dreaptă a matricei și schimbarea elementului curent este imposibilă, atunci matricea are o formă în trepte și putem opri transformarea.

Deoarece matricea este finită dimensiuni, iar într-un pas al algoritmului poziția elementului curent este deplasată la dreapta cu cel puțin o coloană, procesul de transformare se va încheia și în cel mult n pași (n este numărul de coloane din matrice). Aceasta înseamnă că va veni un moment în care matricea va avea o formă în trepte.

Exemplul 10.10. Să transformăm matricea la forma eșalonată folosind transformări elementare de șiruri.

Folosind algoritmul din demonstrația teoremei 10.1 și scriind matricele după finalizarea operațiilor, obținem

Transformări matriceale elementare- sunt transformări ale matricei, în urma cărora se păstrează echivalența matricelor. Astfel, transformările elementare nu modifică setul de soluții al sistemului de ecuații algebrice liniare pe care îl reprezintă această matrice.

Transformările elementare sunt folosite în metoda Gaussiană pentru a reduce o matrice la o formă triunghiulară sau în trepte.

Definiție

Conversii elementare de șiruri sunt numite:

În unele cursuri de algebră liniară, permutarea rândurilor matricei nu se distinge ca o transformare elementară separată datorită faptului că permutarea oricăror două rânduri matricei poate fi obținută prin înmulțirea oricărui rând matricei cu o constantă și adăugând un alt rând la orice rând de matrice înmulțit. printr-o constantă , .

Definit în mod similar transformări elementare ale coloanei.

Transformări elementare reversibil.

Notația indică faptul că matricea poate fi obținută din transformări elementare (sau invers).

Proprietăți

Invarianța de rang în cadrul transformărilor elementare

Echivalența SLAE-urilor în cadrul transformărilor elementare

Hai sa sunăm transformări elementare asupra unui sistem de ecuații algebrice liniare :

• rearanjarea ecuațiilor;
• înmulțirea unei ecuații cu o constantă diferită de zero;
• adunarea unei ecuații la alta, înmulțită cu o constantă.

Acestea. transformări elementare asupra matricei sale extinse. Atunci următoarea afirmație este adevărată: Amintim că două sisteme sunt numite echivalente dacă seturile lor de soluții coincid.

Găsirea matricilor inverse

Teoremă (despre găsirea matricei inverse). Fie determinantul matricei diferit de zero, fie matricea definită prin expresia . Apoi, în timpul unei transformări elementare a rândurilor matricei în matricea de identitate din compoziție, are loc simultan o transformare a.

Reducerea matricilor la formă eșalonată

Să introducem conceptul de matrice pasă: O matrice are vedere în trepte , dacă: Atunci următoarea afirmație este adevărată:

Definiții înrudite

Matrice elementară. Matricea A este elementară dacă înmulțirea unei matrice arbitrare B cu aceasta duce la transformări elementare ale rândurilor din matricea B.

Literatură

Ilyin V. A., Poznyak E. G. Algebră liniară: manual pentru universități. - Ed. a VI-a, șters. - M.: FIZMATLIT, 2004. - 280 p.

Fundația Wikimedia. 2010.

Vedeți ce sunt „Transformările matriceale elementare” în alte dicționare:

Introducere. E. particulele în sensul exact al acestui termen sunt particule primare, în continuare necompuse, din care, prin presupunere, constă toată materia. În modern termenul de fizică „E. h." folosit de obicei nu în sensul său exact, dar mai puțin strict pentru nume... ... Enciclopedie fizică

Introducere. E. particulele în sensul exact al acestui termen sunt particule primare, în continuare necompuse, din care, prin presupunere, constă toată materia. În conceptul „E. h." în fizica modernă ideea de entități primordiale își găsește expresie... ... Marea Enciclopedie Sovietică

Acest termen are alte semnificații, vezi Matrice. Matricea este un obiect matematic scris ca un tabel dreptunghiular de elemente ale unui inel sau câmp (de exemplu, numere întregi, reale sau numere complexe) care reprezintă ... ... Wikipedia

O matrice este un obiect matematic scris sub forma unui tabel dreptunghiular de numere (sau elemente ale unui inel) și care permite operații algebrice (adunare, scădere, înmulțire etc.) între aceasta și alte obiecte similare. Reguli de executare... ... Wikipedia

O matrice este un obiect matematic scris sub forma unui tabel dreptunghiular de numere (sau elemente ale unui inel) și care permite operații algebrice (adunare, scădere, înmulțire etc.) între aceasta și alte obiecte similare. Reguli de executare... ... Wikipedia

O matrice este un obiect matematic scris sub forma unui tabel dreptunghiular de numere (sau elemente ale unui inel) și care permite operații algebrice (adunare, scădere, înmulțire etc.) între aceasta și alte obiecte similare. Reguli de executare... ... Wikipedia

O matrice este un obiect matematic scris sub forma unui tabel dreptunghiular de numere (sau elemente ale unui inel) și care permite operații algebrice (adunare, scădere, înmulțire etc.) între aceasta și alte obiecte similare. Reguli de executare... ... Wikipedia

O matrice este un obiect matematic scris sub forma unui tabel dreptunghiular de numere (sau elemente ale unui inel) și care permite operații algebrice (adunare, scădere, înmulțire etc.) între aceasta și alte obiecte similare. Reguli de executare... ... Wikipedia

Transformările elementare sunt următoarele acțiuni pe rândurile și coloanele matricei A:

1) schimbarea a două rânduri sau coloane ale unei matrice;

2) înmulțirea unui rând sau a unei coloane a unei matrice cu un alt număr decât zero;

3) adăugarea unui alt rând (coloană) la un rând (coloană).

Teorema. Transformările elementare nu schimbă rangul matricei, adică dacă matricea B se obține din matricea A prin transformări elementare, atunci.

Dovada. 1). Când schimbați două coloane ale unei matrice, numărul maxim de coloane liniar independente nu se modifică și, prin urmare, rangul său nu se modifică.

2). Fie ca matricea B să se obțină din matricea A prin înmulțirea rândului i cu numărul t0 și r(A) =k. Evident, orice minor al matricei B care nu conține rândul al i-lea este egal cu minorul corespunzător al matricei A și orice minor al matricei B care conține rândul al ilea este egal cu minorul corespunzător al matricei A înmulțit cu numărul t. In consecinta, minorul de ordin k al matricei B, corespunzator bazei minore a matricei A, va fi diferit de zero, iar toate minorele de ordin k+1 ale matricei B, precum si toate minorele de ordinul k+1 ale matricei. A, va fi egal cu zero. Aceasta înseamnă că r(B)=k=r(A).

3). Fie ca matricea B să fie obținută din matricea A prin adăugarea rândului i la rândul j și r(A) = k. Minorii de ordinul k+1 ale matricei B care nu conțin al-lea rând vor fi egale cu minorele corespunzătoare ale matricei A și, prin urmare, egale cu zero. Minorii de ordinul k+1 ale matricei B care contine randurile i-lea si j-lea vor fi egale cu suma a doi determinanti zero. Unul dintre acești determinanți conține două rânduri identice (rândul j conține elementele rândului i), iar al doilea determinant este un minor de ordinul k+1 al matricei A și, prin urmare, este egal cu zero. Minorii de ordinul k+1 ale matricei B, care conțin al-lea rând, dar care nu conțin al-lea rând, vor fi egale cu suma a două minore de ordinul k+1 ale matricei A și, prin urmare, vor fi egale cu zero. În consecință, toate minorele de ordin k+1 ale matricei B sunt egale cu 0 și r(B)k=r(A).

Fie că matricea C se obține din matricea B prin înmulțirea rândului i cu (-1). Apoi matricea A se obține din matricea C prin adăugarea rândului i la rândul j și înmulțind rândul i cu (-1). Prin urmare, după cum sa dovedit mai sus, va exista r(A)r(C) =r(B). Astfel, inegalitățile r(B)r(A) și r(A)r(B) sunt valide simultan, ceea ce înseamnă că r(A) =r(B).

Această proprietate a transformărilor elementare este folosită în practică pentru a calcula rangul unei matrice. Pentru a face acest lucru, folosind transformări elementare, reducem această matrice (diferită de zero) A la o formă trapezoidală, adică la forma

B= ,

unde elementele pentru toate i = 1,2,...,k; elemente pentru toate i > j și

i > k. Evident, r(B) = k, adică rangul matricei B este egal cu numărul de rânduri non-nule. Aceasta rezultă din faptul că minorul de ordin k al matricei B, situat la intersecția primelor k rânduri și coloane, este un determinant diagonală și este egal cu; și orice minor de ordinul k+1 al matricei B conține un rând zero, ceea ce înseamnă că este egal cu 0 (sau, dacă k = n, nu există deloc astfel de minore).

Teorema. Orice matrice A diferită de zero de dimensiunea mn poate fi redusă la o formă trapezoidală folosind transformări elementare.

Dovada. Deoarece A0, atunci există un element de matrice
. Schimbând primul și i-lea rând, prima și j-a coloană, mutăm elementul în colțul din stânga sus al matricei și notează
. Apoi la i-lea rând al matricei rezultate (i= 2,3, ...,m) adunăm primul rând înmulțit cu numărul . În urma acestor transformări elementare, obținem matricea

A
.

Dacă toate elementele
matricele A sunt egale cu zero, atunci se demonstrează teorema. Dacă există un element
, apoi, prin rearanjarea al doilea și al i-lea rând, a doua și j-a coloană a matricei A, mutăm elementul în locul elementului si denota
(Dacă
, apoi notăm imediat
). Apoi la rândul i al matricei rezultate (i= 3, ...,m) adunăm al doilea rând înmulțit cu numărul . Ca rezultat, obținem matricea

.

Continuând acest proces, într-un număr finit de pași obținem matricea B, adică reducem matricea A la o formă trapezoidală.

Exemplu. Să calculăm rangul matricei



. Săgețile indică următoarele transformări elementare: 1) prima și a doua linie au fost schimbate; 2) a adăugat o a treia la a patra linie; 3) a adăugat prima linie, înmulțită cu -2, la a treia linie și a împărțit a patra linie la 3; 4) a împărțit a treia linie la 5 și a schimbat a treia și a patra linie; 5) o a doua linie a fost adăugată la a treia linie, înmulțită cu -3, și o a treia a fost adăugată la a patra linie. Se poate observa că matricea obţinută din matricea A prin transformările elementare indicate are formă trapezoidală cu trei rânduri nenule. Prin urmare, r(A) = 3.

Transformări matriceale elementare- sunt transformări ale matricei, în urma cărora se păstrează echivalența matricelor. Astfel, transformările elementare nu modifică setul de soluții al sistemului de ecuații algebrice liniare pe care îl reprezintă această matrice.

Transformările elementare sunt folosite în metoda Gaussiană pentru a reduce o matrice la o formă triunghiulară sau în trepte.

Definiție

Conversii elementare de șiruri sunt numite:

În unele cursuri de algebră liniară, permutarea rândurilor de matrice nu este separată într-o transformare elementară separată, datorită faptului că permutarea oricăror două rânduri de matrice poate fi obținută prin înmulțirea oricărui rând de matrice cu o constantă. k (\displaystyle k), și adăugând la orice rând al matricei un alt rând, înmulțit cu o constantă k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

Definit în mod similar transformări elementare ale coloanei.

Transformări elementare reversibil.

Notația indică faptul că matricea A (\displaystyle A) poate fi obtinut de la B (\displaystyle B) prin transformări elementare (sau invers).

Proprietăți

Invarianța de rang în cadrul transformărilor elementare

Teorema (asupra invarianței rangului sub transformări elementare). Dacă A ∼ B (\displaystyle A\sim B), Acea r a n g A = r a n g B (\displaystyle \mathrm (sunet) A=\mathrm (sunet) B).

Echivalența SLAE-urilor în cadrul transformărilor elementare

Hai sa sunăm transformări elementare asupra unui sistem de ecuații algebrice liniare :

• rearanjarea ecuațiilor;
• înmulțirea unei ecuații cu o constantă diferită de zero;
• adunarea unei ecuații la alta, înmulțită cu o constantă.

Adică transformări elementare peste matricea sa extinsă. Atunci următoarea afirmație este adevărată: Amintim că două sisteme sunt numite echivalente dacă seturile lor de soluții coincid.

Găsirea matricilor inverse

Teoremă (despre găsirea matricei inverse). Fie determinantul matricei A n × n (\displaystyle A_(n\times n)) nu este egal cu zero, fie matricea B (\displaystyle B) este determinată de expresie B = [ A | E ] n × 2 n (\displaystyle B=_(n\times 2n)). Apoi, cu o transformare elementară a rândurilor matricei A (\displaystyle A) la matricea identitară E (\displaystyle E) ca parte din B (\displaystyle B) transformarea are loc în același timp E (\displaystyle E) La A - 1 (\displaystyle A^(-1)).