Aké elementárne transformácie je možné vykonať pomocou matice. Maticová algebra - elementárne transformácie matíc. Matica, typy matíc, operácie s maticami
Základnéreťazcové konverzie matice sa nazývajú transformácie nasledujúcich typov:
1) Vynásobenie každého prvku reťazca rovnakým nenulovým číslom. Zostávajúce reťazce zostanú nezmenené (v skratke: vynásobenie reťazca číslom).
2) Pridanie zodpovedajúcich prvkov iného riadku ku každému prvku určitého riadku, vynásobené rovnakým číslom. Zostávajúce riadky (vrátane pridávaného) zostanú nezmenené (v skratke: pridanie ďalšieho riadku do riadku, vynásobené číslom).
3) Vymeňte niektoré dva riadky matice. Zvyšné riadky zostávajú nezmenené.
Tieto premeny sa nazývajú resp premeny prvého , druhý A tretí typ (druh ). Ak ich aplikujeme postupne, získame zložitejšie transformácie.
Podobne definované transformácie elementárnych stĺpcov matice.
Veta
Transformácia tretieho typu je kombináciou transformácií prvého a druhého typu.
Transformácie tretieho typu teda možno klasifikovať ako zložitejšie ako elementárne. Ale stále sa to považuje za základné kvôli pohodliu.
Veta
Každá matica môže byť zredukovaná na stupňovitú maticu pomocou elementárnych riadkových transformácií. Ak na maticu aplikujeme elementárne transformácie riadkov a stĺpcov, potom sa môže zredukovať na lichobežníkový tvar.
Napríklad,
á(1) Prehoďte prvý a druhý riadok (transformácia tretieho typu).
(2) Prvý riadok, vynásobený 2, bol pridaný k druhému a odčítaný od tretieho, vynásobený 3, pridaný k štvrtému (transformácie druhého typu).
(3) Druhý riadok bol odpočítaný od tretieho a druhý riadok vynásobený 14/11 bol odpočítaný od štvrtého.
(4) Vymeňte tretí a štvrtý riadok.ñ
Takto sme transformovali pôvodnú maticu
postupným spôsobom
Teraz, keď sme vymenili druhý a tretí stĺpec a potom ho vymenili za štvrtý stĺpec, presunieme druhý stĺpec na miesto štvrtého, tretí a štvrtý stĺpec budú na miesto druhého a tretieho stĺpca:
čím sa pôvodná matrica premení na lichobežníkovú.
Cvičenia
Priveďte matricu do stupňovitého a lichobežníkového tvaru:
Nasledujúce tri operácie sú tzv elementárne transformácie riadkov matice:
1) Násobenie i-tý riadok matice pre číslo λ ≠ 0:
ktoré budeme písať v tvare (i) → λ(i).
2) Permutácia dvoch riadkov v matici, napríklad i-tého a k-tého riadku:
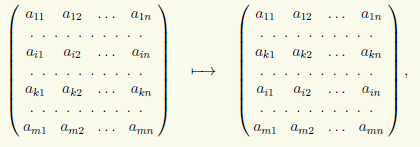
ktorý budeme písať v tvare (i) ↔ (k).
3) Do i-teho riadku matice pripočítame jej k-tý riadok s koeficientom λ:
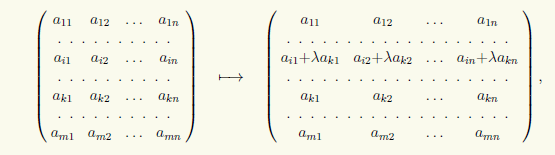
ktoré budeme písať v tvare (i) → (i) + λ(k).
Podobné operácie so stĺpcami matice sa nazývajú transformácie elementárnych stĺpcov.
Každá elementárna transformácia riadkov alebo stĺpcov matice má inverzná elementárna transformácia, ktorý transformovanú maticu zmení na pôvodnú. Napríklad inverzná transformácia pre permutáciu dvoch reťazcov je permutácia rovnakých reťazcov.
Každú elementárnu transformáciu riadkov (stĺpcov) matice A možno interpretovať ako násobenie A vľavo (vpravo) maticou špeciálneho tvaru. Táto matica sa získa, ak sa vykoná rovnaká transformácia matica identity. Pozrime sa bližšie na prevody elementárnych reťazcov.
Nech je výsledkom matica B i-té násobenie riadkov matice A typu m×n číslom λ ≠ 0. Potom B = E i (λ)A, kde maticu E i (λ) získame z matice identity E rádu m vynásobením jej i- riadok číslom λ.
Nech získame maticu B ako výsledok permutácie i-tého a k-tého riadku matice A typu m×n. Potom B = F ik A, kde maticu F ik získame z matice identity E rádu m permutáciou jej i-tého a k-tého riadku.
Nech maticu B získame pripočítaním jej k-tého riadku s koeficientom λ k i-tému riadku matice A m×n. Potom B = G ik (λ)А, kde maticu G ik získame z matice identity E rádu m pripočítaním k-tého riadku s koeficientom λ k i-temu riadku, t.j. v priesečníku i-tého riadku a k-tého stĺpca matice E sa nulový prvok nahradí číslom λ.
Elementárne transformácie stĺpcov matice A sú realizované úplne rovnako, no zároveň je násobená maticami špeciálneho typu nie vľavo, ale vpravo.
Pomocou algoritmov, ktoré sú založené na elementárnych transformáciách riadkov a stĺpcov, možno matice transformovať na rôzne druhy. Jeden z najdôležitejších takýchto algoritmov tvorí základ dôkazu nasledujúcej vety.
Veta 10.1. Pomocou elementárnych riadkových transformácií je možné zredukovať akúkoľvek maticu stupňovitý pohľad.
◄ Dôkaz vety spočíva v konštrukcii špecifický algoritmus uvedenie matrice do stupňovitej formy. Tento algoritmus pozostáva z opakovaného opakovania v určitom poradí troch operácií spojených s niektorým aktuálnym prvkom matice, ktorý je vybraný na základe jeho umiestnenia v matici. V prvom kroku algoritmu vyberieme ľavý horný ako aktuálny prvok matice, t.j. [A] 11.
1*. Ak je aktuálny prvok nula, prejdite na operáciu 2*. Ak sa nerovná nule, riadok, v ktorom sa nachádza aktuálny prvok (aktuálny riadok), sa pripočíta s príslušnými koeficientmi k riadkom umiestneným nižšie, takže všetky prvky matice v stĺpci pod aktuálnym prvkom sa stanú nulovými. Napríklad, ak je aktuálny prvok [A] ij , potom ako koeficient pre k-tý riadok, k = i + 1, ... , by sme mali vziať číslo - [A] kj /[A] ij . Vyberieme nový aktuálny prvok, posunieme sa v matici o jeden stĺpec doprava a o jeden riadok nadol a pokračujeme k ďalšiemu kroku zopakovaním operácie 1*. Ak takýto posun nie je možný, t.j. bol dosiahnutý posledný stĺpec alebo riadok, prestaneme transformovať.
2*. Ak sa aktuálny prvok v niektorom riadku matice rovná nule, potom sa pozrieme na prvky matice umiestnené v stĺpci pod aktuálnym prvkom. Ak medzi nimi nie sú nenulové jednotky, pristupujeme k operácii 3*. Vpustiť k-tá čiara pod aktuálnym prvkom je nenulový prvok. Vymeňte aktuálne a k-tá čiara a vrátiť sa do prevádzky 1*.
3*. Ak sa aktuálny prvok a všetky prvky pod ním (v tom istom stĺpci) rovnajú nule, zmeníme aktuálny prvok a posunieme v matici o jeden stĺpec doprava. Ak je takýto posun možný, t. j. aktuálny prvok nie je v stĺpci matice úplne vpravo, zopakujeme operáciu 1*. Ak sme už dosiahli pravý okraj matice a zmena aktuálneho prvku nie je možná, potom má matica stupňovitý tvar a môžeme prestať transformovať.
Keďže matica má konečnú rozmery a v jednom kroku algoritmu sa pozícia aktuálneho prvku posunie doprava aspoň o jeden stĺpec, proces transformácie sa ukončí, a to maximálne v n krokoch (n je počet stĺpcov v matici). To znamená, že príde chvíľa, keď matica bude mať stupňovitú formu.
Príklad 10.10. Poďme transformovať maticu 
do echelónového tvaru pomocou elementárnych reťazcových transformácií.
Použitím algoritmu z dôkazu vety 10.1 a zápisu matíc po dokončení jeho operácií dostaneme
Elementárne maticové transformácie- ide o transformácie matice, v dôsledku čoho je zachovaná ekvivalencia matíc. Elementárne transformácie teda nemenia množinu riešení sústavy lineárnych algebraických rovníc, ktoré táto matica predstavuje.
Elementárne transformácie sa používajú v Gaussovej metóde na redukciu matice na trojuholníkový alebo stupňovitý tvar.
Definícia
Konverzie elementárnych reťazcov sa volajú:
V niektorých kurzoch lineárnej algebry sa permutácia riadkov matice nerozlišuje ako samostatná elementárna transformácia v dôsledku skutočnosti, že permutáciu ľubovoľných dvoch riadkov matice možno získať vynásobením ľubovoľného riadka matice konštantou a pridaním ďalšieho riadka k ľubovoľnému vynásobenému riadku matice. konštantou , .
Podobne definované transformácie elementárnych stĺpcov.
Elementárne transformácie reverzibilné.
Zápis naznačuje, že maticu možno získať elementárnymi transformáciami (alebo naopak).
Vlastnosti
Invariantnosť poradia pri elementárnych transformáciách
Ekvivalencia SLAE pri elementárnych transformáciách
Zavolajme elementárne transformácie nad sústavou lineárnych algebraických rovníc :- preskupenie rovníc;
- násobenie rovnice nenulovou konštantou;
- pridanie jednej rovnice k druhej, vynásobené nejakou konštantou.
Hľadanie inverzných matíc
| Veta (o hľadaní inverznej matice). Nech je determinant matice nenulový, nech je matica definovaná výrazom . Potom počas elementárnej transformácie riadkov matice na maticu identity v kompozícii súčasne nastáva transformácia na. |
Redukcia matíc na echelonový tvar
Predstavme si pojem krokových matíc: Matica má stupňovitý pohľad , ak: Potom platí nasledujúce tvrdenie:Súvisiace definície
Elementárna matica. Matica A je elementárna, ak ňou vynásobenie ľubovoľnej matice B vedie k elementárnym transformáciám riadkov v matici B.
Literatúra
Ilyin V. A., Poznyak E. G. Lineárna algebra: Učebnica pre vysoké školy. - 6. vyd., vymazané. - M.: FIZMATLIT, 2004. - 280 s.
Nadácia Wikimedia. 2010.
Pozrite sa, čo sú „Elementárne maticové transformácie“ v iných slovníkoch:
Úvod. E. častice v presnom význame tohto pojmu sú primárne, ďalej nerozložiteľné častice, z ktorých sa podľa predpokladu skladá všetka hmota. V modernom fyzikálny termín „E. h." zvyčajne sa nepoužíva v presnom význame, ale menej striktne pre meno... ... Fyzická encyklopédia
Úvod. E. častice v presnom význame tohto pojmu sú primárne, ďalej nerozložiteľné častice, z ktorých sa podľa predpokladu skladá všetka hmota. V koncepte „E. h." v modernej fyzike nachádza myšlienka prvotných entít vyjadrenie... ... Veľká sovietska encyklopédia
Tento výraz má iné významy, pozri Matrix. Matrix je matematický objekt napísaný ako obdĺžniková tabuľka prvkov kruhu alebo poľa (napríklad celé čísla, reálne čísla alebo komplexné čísla), ktorý predstavuje ... ... Wikipedia
Matica je matematický objekt napísaný vo forme obdĺžnikovej tabuľky čísel (alebo prvkov krúžku) a umožňujúci algebraické operácie (sčítanie, odčítanie, násobenie atď.) medzi ním a inými podobnými objektmi. Pravidlá vykonávania... ... Wikipedia
Matica je matematický objekt napísaný vo forme obdĺžnikovej tabuľky čísel (alebo prvkov krúžku) a umožňujúci algebraické operácie (sčítanie, odčítanie, násobenie atď.) medzi ním a inými podobnými objektmi. Pravidlá vykonávania... ... Wikipedia
Matica je matematický objekt napísaný vo forme obdĺžnikovej tabuľky čísel (alebo prvkov krúžku) a umožňujúci algebraické operácie (sčítanie, odčítanie, násobenie atď.) medzi ním a inými podobnými objektmi. Pravidlá vykonávania... ... Wikipedia
Matica je matematický objekt napísaný vo forme obdĺžnikovej tabuľky čísel (alebo prvkov krúžku) a umožňujúci algebraické operácie (sčítanie, odčítanie, násobenie atď.) medzi ním a inými podobnými objektmi. Pravidlá vykonávania... ... Wikipedia
Matica je matematický objekt napísaný vo forme obdĺžnikovej tabuľky čísel (alebo prvkov krúžku) a umožňujúci algebraické operácie (sčítanie, odčítanie, násobenie atď.) medzi ním a inými podobnými objektmi. Pravidlá vykonávania... ... Wikipedia
Elementárne transformácie sú nasledujúce akcie s riadkami a stĺpcami matice A:
1) výmena dvoch riadkov alebo stĺpcov matice;
2) násobenie riadku alebo stĺpca matice číslom iným ako nula;
3) pridanie ďalšieho riadku (stĺpca) do jedného riadku (stĺpca).
Veta. Elementárne transformácie nemenia poradie matice, teda ak maticu B získame z matice A elementárnymi transformáciami, potom.
Dôkaz. 1). Pri zámene dvoch stĺpcov matice sa maximálny počet lineárne nezávislých stĺpcov nemení, a preto sa nemení ani jej poradie.
2). Nech maticu B získame z matice A vynásobením i-tého riadku číslom t0 a r(A) =k. Je zrejmé, že každá minorita matice B, ktorá neobsahuje i-tý riadok, sa rovná zodpovedajúcej minoritnej skupine matice A a každá minoritná skupina matice B obsahujúca i-tý riadok sa rovná zodpovedajúcej minoritnej skupine matice A vynásobenej číslom t. V dôsledku toho bude minorita rádu k matice B, zodpovedajúca minoritnej báze matice A, nenulová a všetky minority rádu k+1 matice B, ako aj všetky minority rádu k+1 matice A, sa bude rovnať nule. To znamená, že r(B)=k=r(A).
3). Nech maticu B získame z matice A pridaním i-tého riadku k j-tému riadku a r(A) = k. Vedľajšie hodnoty rádu k+1 matice B, ktoré neobsahujú j-tý riadok, sa budú rovnať zodpovedajúcim vedľajším položkám matice A, a teda rovné nule. Vedľajšie hodnoty rádu k+1 matice B obsahujúcej i-tý a j-tý riadok sa budú rovnať súčtu dvoch nulových determinantov. Jeden z týchto determinantov obsahuje dva identické riadky (j-tý riadok obsahuje prvky i-teho riadku) a druhý determinant je minoritou rádu k+1 matice A, a preto sa rovná nule. Vedľajšie hodnoty rádu k+1 matice B obsahujúcej j-tý riadok, ale neobsahujúce i-tý riadok, sa budú rovnať súčtu dvoch menších rádu k+1 matice A, a preto sa budú rovnať nula. V dôsledku toho sa všetky minority rádu k+1 matice B rovnajú 0 a r(B)k=r(A).
Nech maticu C získame z matice B vynásobením i riadku (-1). Potom sa matica A získa z matice C pridaním i-teho riadku k j-tému riadku a vynásobením i-tého riadku (-1). Preto, ako bolo dokázané vyššie, bude existovať r(A)r(C) =r(B). Nerovnice r(B)r(A) a r(A)r(B) teda platia súčasne, čo znamená, že r(A) =r(B).
Táto vlastnosť elementárnych transformácií sa v praxi využíva na výpočet hodnosti matice. Aby sme to dosiahli, pomocou elementárnych transformácií zredukujeme túto (nenulovú) maticu A do lichobežníkového tvaru, teda do tvaru
B= 
,
kde prvky pre všetky i = 1,2,...,k; prvky pre všetky i > j a
i > k. Je zrejmé, že r(B) = k, to znamená, že poradie matice B sa rovná počtu nenulových riadkov. Vyplýva to zo skutočnosti, že minorita rádu k matice B, ktorá sa nachádza v priesečníku prvých k riadkov a stĺpcov, je diagonálnym determinantom a rovná sa; a akákoľvek vedľajšia matica k+1 matice B obsahuje nulový riadok, čo znamená, že sa rovná 0 (alebo ak k = n, takéto minority vôbec neexistujú).
Veta. Akákoľvek nenulová matica A rozmeru mn môže byť pomocou elementárnych transformácií redukovaná na lichobežníkový tvar.
Dôkaz. Pretože A0, potom existuje prvok matice 
. Zámenou prvého a i-teho riadku, prvého a j-tého stĺpca presunieme prvok 
do ľavého horného rohu matice a označte 
. Potom k i-temu riadku výslednej matice (i= 2,3, ...,m) pripočítame prvý riadok vynásobený číslom 
. V dôsledku týchto elementárnych transformácií získame maticu
A 
.
Ak všetky prvky 
matice A sa rovnajú nule, potom je veta dokázaná. Ak existuje prvok 
, potom preusporiadaním druhého a i-teho riadku, druhého a j-tého stĺpca matice A presunieme prvok 
namiesto prvku 
a označujú 
(Ak 
, potom hneď označujeme 
). Potom k i-temu riadku výslednej matice (i= 3, ...,m) pridáme druhý riadok vynásobený číslom 
. V dôsledku toho dostaneme maticu
.
Pokračujúc v tomto procese, v konečnom počte krokov získame maticu B, to znamená, že maticu A zredukujeme na lichobežníkový tvar.
Príklad. Vypočítajme hodnosť matice
. Šípky označujú nasledujúce elementárne transformácie: 1) prvý a druhý riadok boli prehodené; 2) pridal tretí do štvrtého riadku; 3) pridal prvý riadok, vynásobený -2, k tretiemu riadku a vydelil štvrtý riadok 3; 4) delili tretí riadok 5 a prehodili tretí a štvrtý riadok; 5) k tretiemu riadku bol pridaný druhý riadok, vynásobený -3, a tretí bol pridaný k štvrtému riadku. Je vidieť, že matica získaná z matice A uvedenými elementárnymi transformáciami má lichobežníkový tvar s tromi nenulovými riadkami. Preto r(A) = 3.
Elementárne maticové transformácie- ide o transformácie matice, v dôsledku čoho je zachovaná ekvivalencia matíc. Elementárne transformácie teda nemenia množinu riešení sústavy lineárnych algebraických rovníc, ktoré táto matica predstavuje.
Elementárne transformácie sa používajú v Gaussovej metóde na redukciu matice na trojuholníkový alebo stupňovitý tvar.
Definícia
Konverzie elementárnych reťazcov sa volajú:
V niektorých kurzoch lineárnej algebry nie je permutácia riadkov matice rozdelená do samostatnej elementárnej transformácie v dôsledku skutočnosti, že permutáciu akýchkoľvek dvoch riadkov matice možno získať vynásobením ľubovoľného riadka matice konštantou k (\displaystyle k), a pridanie do ľubovoľného riadku matice ďalší riadok, vynásobený konštantou k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).
Podobne definované transformácie elementárnych stĺpcov.
Elementárne transformácie reverzibilné.
Zápis označuje, že matica A (\displaystyle A) možno získať z B (\displaystyle B) prostredníctvom elementárnych transformácií (alebo naopak).
Vlastnosti
Invariantnosť poradia pri elementárnych transformáciách
| Veta (o invariancii poradia pri elementárnych transformáciách). Ak A ∼ B (\displaystyle A\sim B), To r a n g A = r a n g B (\displaystyle \mathrm (rang) A=\mathrm (rang) B). |
Ekvivalencia SLAE pri elementárnych transformáciách
Zavolajme elementárne transformácie nad sústavou lineárnych algebraických rovníc :- preskupenie rovníc;
- násobenie rovnice nenulovou konštantou;
- pridanie jednej rovnice k druhej, vynásobené nejakou konštantou.
Hľadanie inverzných matíc
| Veta (o hľadaní inverznej matice). Nech je determinant matice A n × n (\displaystyle A_(n\krát n)) sa nerovná nule, nech je matica B (\displaystyle B) je určený výrazom B = [ A | E ] n × 2 n (\displaystyle B=_(n\krát 2n)). Potom s elementárnou transformáciou riadkov matice A (\displaystyle A) do matrice identity E (\displaystyle E) ako súčasť B (\displaystyle B) transformácia prebieha súčasne E (\displaystyle E) Komu A − 1 (\displaystyle A^(-1)). |
