Які елементарні перетворення можна виконувати із матрицею. Матрична алгебра – елементарні перетворення матриць. Матриця, види матриць, дії над матрицями

Елементарнними перетвореннями рядківматриці називається перетворення наступних типів:

1) Розмноження кожного елемента деякого рядка на те саме ненульове число. Інші рядки залишаються без зміни (коротко: множення рядка на число).

2) Додаток до кожного елемента деякого рядка відповідних елементів іншого рядка, помножені на те саме число. Інші рядки (у тому числі і додається) залишаються без зміни (коротко: додаток до рядка іншого, помноженого на число).

3) Зміна місцями деяких двох рядків матриці. Інші рядки залишаються без зміни.

Ці перетворення називаються відповідно перетвореннями першого , другого і третього типу (роду ). Послідовно застосовуючи їх, ми отримуємо складніші перетворення.

Аналогічно визначаються елементарні перетворення стовпців матриці.

Теорема

Перетворення третього типу є деякою комбінацією перетворень першого та другого типів.

Таким чином, перетворенням третього типу можна віднести до складніших, ніж елементарні. Але його прийнято все-таки вважати елементарним задля зручності.

Теорема

Будь-яку матрицю елементарними перетвореннями рядків можна призвести до ступінчастої. Якщо до матриці застосувати елементарні перетворення рядків та стовпців, то її можна привести до трапецієдальному вигляду.

Наприклад,

á(1) Поміняли місцями перший і другий рядки (перетворення третього типу).

(2) Перший рядок, помножений на 2, додали до другого і відняли з третього, помножений на 3, додали до четвертого (перетворення другого типу).

(3) Другий рядок відняли з третього та другий рядок, помножений на 14/11 віднімали з четвертого.

(4) Поміняли місцями третій і четвертий рядки.

Таким чином, перетворили вихідну матрицю

у ступінчасту

Тепер, помінявши місцями другий і третій стовпець, а потім помінявши його з четвертим стовпцем, переміщаємо другий стовпець на місце четвертого, третій і четвертий стовпці виявляться відповідно на місці другого і третього стовпців:

тим самим перетворили вихідну матрицю на трапецієдальну.

Вправи

Привести матрицю до ступінчастого та трапецієдального видів:

Наступні три операції називають елементарними перетвореннями рядків матриці:

1) Множення i-го рядкаматриці на число λ ≠ 0:

яке записуватимемо у вигляді (i) → λ(i).

2) Перестановка двох рядків у матриці, наприклад i-й та k-й рядків:

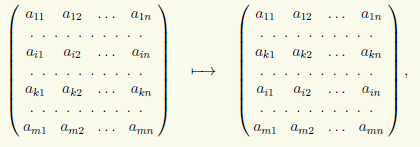
яку записуватимемо у вигляді (i) ↔ (k).

3) Додавання до i-го рядка матриці її k-го рядка з коефіцієнтом λ:

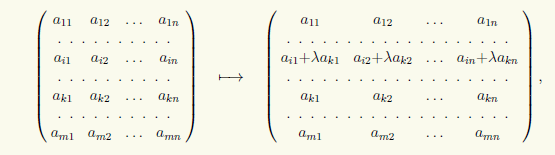
що записуватимемо у вигляді (i) → (i) + λ(k).

Аналогічні операції над стовпцями матриці називають елементарними перетвореннями стовпців.

Кожне елементарне перетворення рядків чи стовпців матриці має зворотне елементарне перетворення, яке перетворену матрицю перетворює на вихідну. Наприклад, зворотним перетворенням для перестановки двох рядків є перестановка тих самих рядків.

Кожне елементарне перетворення рядків (стовпців) матриці можна трактувати як множення A зліва (праворуч) на матрицю спеціального виду. Ця матриця виходить, якщо те ж перетворення виконати над одиничною матрицею. Розглянемо детальніше елементарні перетворення рядків.

Нехай матриця B виходить у результаті множення i-йрядки матриці типу A m×n на число λ ≠ 0. Тоді B = Е i (λ)А, де матриця Е i (λ) виходить з одиничної матриці E порядку m множенням її i-го рядка на число λ.

Нехай матриця B виходить в результаті перестановки i-ї та k-ї рядків матриці типу А m×n. Тоді B = F ik А де матриця F ik виходить з одиничної матриці E порядку m перестановкою її i-й і k-й рядків.

Нехай матриця B виходить в результаті додавання до i-го рядка матриці типу А m×n її k-го рядка з коефіцієнтом λ. Тоді B = G ik (λ)А, де матриця G ik виходить з одиничної матриці E порядку m в результаті додавання до i-го рядка k-го рядка з коефіцієнтом λ, тобто. на перетині i-го рядка і k-го стовпця матриці E нульовий елемент замінений число λ.

Так само реалізуються елементарні перетворення стовпців матриці A, але при цьому вона множиться на матриці спеціального виду не зліва, а справа.

За допомогою алгоритмів, що ґрунтуються на елементарних перетвореннях рядків та стовпців, матриці можна перетворювати до різного вигляду. Один із найважливіших таких алгоритмів становить основу доказу наступної теореми.

Теорема 10.1.За допомогою елементарних перетворень рядків будь-яку матрицю можна привести до східчастого вигляду.

◄ Доказ теореми полягає у побудові конкретного алгоритмуприведення матриці до ступінчастого вигляду. Цей алгоритм полягає у багаторазовому повторенні у певному порядку трьох операцій, пов'язаних з деяким поточним елементом матриці, який вибирається виходячи з розташування у матриці. У першому кроці алгоритму як поточного елемента матриці вибираємо верхній лівий, тобто. [A] 11 .

1*. Якщо поточний елемент дорівнює нулю, то переходимо до операції 2*. Якщо ж він не дорівнює нулю, то рядок, в якому розташований поточний елемент (поточний рядок), додаємо з відповідними коефіцієнтами до рядків, розташованих нижче, так, щоб усі елементи матриці, що стоять у стовпці під поточним елементом, звернулися до нуля. Наприклад, якщо поточний елемент є [A] ij , то як коефіцієнт для k-го рядка, k = i + 1, ... , нам слід взяти число - [A] kj /[A] ij . Вибираємо новий поточний елемент, зміщуючись у матриці на один стовпець праворуч і на один рядок вниз, і переходимо до наступного кроку, повторюючи операцію 1*. Якщо таке усунення неможливе, тобто. досягнутий останній стовпець або рядок, перетворення припиняємо.

2*. Якщо поточний елемент у певному рядку матриці дорівнює нулю, переглядаємо елементи матриці, розташовані в стовпці під поточним елементом. Якщо серед них немає ненульових, переходимо до операції 3*. Нехай у k-му рядкупід поточним елементом знаходиться ненульовий елемент. Змінюємо місцями поточну та k-му рядкута повертаємося до операції 1*.

3*. Якщо поточний елемент і всі елементи під ним (у тому самому стовпці) дорівнюють нулю, змінюємо поточний елемент, зміщуючись в матриці на один стовпець праворуч. Якщо таке усунення можливе, т. е. поточний елемент перебуває над правому стовпці матриці, то повторюємо операцію 1* . Якщо ми вже досягли правого краю матриці і зміна поточного елемента неможлива, то матриця має ступінчастий вигляд, і ми можемо припинити перетворення.

Так як матриця має кінцеві розміриа за один крок алгоритму положення поточного елемента зміщується вправо хоча б на один стовпець, процес перетворень закінчиться, причому не більше ніж за n кроків (n - кількість стовпців у матриці). Значить, настане момент, коли матриця матиме ступінчастий вигляд.

Приклад 10.10.Перетворимо матрицю до ступінчастого вигляду за допомогою елементарних перетворень рядків.

Використовуючи алгоритм із доказу теореми 10.1 та записуючи матриці після закінчення виконання його операцій, отримуємо

Елементарні перетворення матриці- це перетворення матриці , у яких зберігається еквівалентність матриць. Таким чином, елементарні перетворення не змінюють безліч рішень системи лінійних рівнянь алгебри , яку представляє ця матриця.

Елементарні перетворення використовуються у методі Гауса для приведення матриці до трикутного або ступінчастого вигляду.

Визначення

Елементарними перетвореннями рядківназивають:

У деяких курсах лінійної алгебри перестановка рядків матриці не виділяється в окреме елементарне перетворення через те, що перестановку місцями будь-яких двох рядків матриці можна отримати, використовуючи множення будь-якого рядка матриці на константу , і додавання до будь-якого рядка матриці іншого рядка, помноженого на константу .

Аналогічно визначаються елементарні перетворення стовпців.

Елементарні перетворення оборотні.

Позначення вказує на те, що матриця може бути отримана шляхом елементарних перетворень (або навпаки).

Властивості

Інваріантність рангу при елементарних перетвореннях

Еквівалентність СЛАУ при елементарних перетвореннях

Назвемо елементарними перетвореннями над системою лінійних рівнянь алгебри :

• перестановку рівнянь;
• множення рівняння на ненульову константу;
• складання одного рівняння з іншим, помноженим на деяку константу.

Тобто. елементарні перетворення над її розширеною матрицею. Тоді справедливе наступне твердження: Нагадаємо, що дві системи називаються еквівалентними, якщо множини їх рішень збігаються.

Знаходження зворотних матриць

Теорема (про знаходження зворотної матриці). Нехай визначник матриці не дорівнює нулю, нехай матриця визначається виразом . Тоді при елементарному перетворенні рядків матриці до одиничної матриці у складі одночасно відбувається перетворення до .

Приведення матриць до східчастого вигляду

Введемо поняття ступінчастих матриць: Матриця має східчастий вигляд якщо: Тоді справедливе наступне твердження:

Пов'язані визначення

Елементарна матриця.Матриця А є елементарною, якщо множення на неї довільної матриці призводить до елементарним перетворенням рядків у матриці В.

Література

Ільїн В. А., Позняк Е. Г. Лінійна алгебра: Підручник для вузів. - 6-те вид., Стер. – М.: ФІЗМАТЛІТ, 2004. – 280 с.

Wikimedia Foundation.

2010 .

Вступ. е. ч. в точному значенні цього терміна первинні, далі нерозкладні ч ци, з яких, за припущенням, складається вся матерія. У совр. фізики термін «Е. ч.» зазвичай використовується над своєму точному значенні, а менш строго для наименования… … Фізична енциклопедія

Вступ. е. ч. у точному значенні цього терміна первинні, далі нерозкладні частинки, з яких, за припущенням, складається вся матерія. У понятті «Е. ч.» у сучасній фізиці знаходить вираження ідея про першорядні сутності, … Велика Радянська Енциклопедія

Цей термін має й інші значення, див. Матриця. Матриця математичний об'єкт, що записується у вигляді прямокутної таблиці елементів кільця чи поля (наприклад, цілих, дійсних чи комплексних чисел), яка представляє… Вікіпедія

Матриця математичний об'єкт, записуваний як прямокутної таблиці чисел (чи елементів кільця) і допускає алгебраїчні операції (складення, віднімання, множення та інших.) між ним та інші подібними об'єктами. Правила виконання… … Вікіпедія

Матриця математичний об'єкт, записуваний як прямокутної таблиці чисел (чи елементів кільця) і допускає алгебраїчні операції (складення, віднімання, множення та інших.) між ним та інші подібними об'єктами. Правила виконання… … Вікіпедія

Матриця математичний об'єкт, записуваний як прямокутної таблиці чисел (чи елементів кільця) і допускає алгебраїчні операції (складення, віднімання, множення та інших.) між ним та інші подібними об'єктами. Правила виконання… … Вікіпедія

Матриця математичний об'єкт, записуваний як прямокутної таблиці чисел (чи елементів кільця) і допускає алгебраїчні операції (складення, віднімання, множення та інших.) між ним та інші подібними об'єктами. Правила виконання… … Вікіпедія

Матриця математичний об'єкт, записуваний як прямокутної таблиці чисел (чи елементів кільця) і допускає алгебраїчні операції (складення, віднімання, множення та інших.) між ним та інші подібними об'єктами. Правила виконання… … Вікіпедія

Елементарними перетвореннями називають такі дії над рядками та стовпцями матриці A:

1) перестановку місцями двох рядків чи стовпців матриці;

2) множення рядка або стовпця матриці на число, відмінне від нуля;

3) додаток до одного рядка (стовпця) іншого рядка (стовпця).

Теорема.Елементарні перетворення не змінюють ранг матриці, тобто якщо матриця B отримана з матриці A елементарними перетвореннями, то.

Доведення. 1). При перестановці місцями двох стовпців матриці максимальне число лінійно незалежних стовпців не змінюється, отже, не змінюється її ранг.

2). Нехай матриця B отримана з матриці A множенням i-го рядка на число t0 іr(A) =k. Очевидно, будь-який мінор матриці B, що не містить i-те рядок, дорівнює відповідному мінору матриці A, а будь-який мінор матриці B, що містить i-ту рядок, дорівнює відповідному мінору матриці A помноженому на число t. Отже, мінор порядку k матриці B, відповідний базисному мінору матриці A, буде відмінний від нуля, а всі мінори порядку k +1 матриці B, як і всі мінори порядку k + 1 матриці A, дорівнюватимуть нулю. А це означає, що r(B)=k=r(A).

3). Нехай матриця B отримана з матриці A додаваннямi-ого рядка доj-того рядка r(A) =k. Мінори порядку k+1 матриці B, що не містять j-ту рядок, дорівнюють відповідним мінорам матриці A, і тому дорівнюють нулю. Мінори порядку k+1 матриці B, що містять i-ту іj-ту рядки, дорівнюватимуть сумі двох нульових визначників. Один з цих визначників містить два однакових рядки (вj-тому рядку розташовані елементиi–того рядка), а другий визначник є мінором порядкуk+1 матриціAі тому дорівнює нулю. Мінори порядку k + 1 матриці B, що містять j-ту рядок, але не містять i - той рядок, дорівнюватимуть сумі двох мінорів порядку k + 1 матриці A і тому теж будуть рівні нулю. Отже, всі мінори порядку k+1 матриці B дорівнюють 0 і r(B)k=r(A).

Нехай матриця отримана з матриціBмноженням i–того рядка на (-1). Тоді матриця A виходить з матриці C додаваннямi-того рядка доj-того рядка і множеннямi-того рядка на (-1). Отже, як було доведено вище, r(A)r(C) =r(B). Таким чином, одночасно справедливі нерівності r(B)r(A) іr(A)r(B) звідки випливає, щоr(A) =r(B).

Цю властивість елементарних перетворень використовують практично для обчислення рангу матриці. Для цього за допомогою елементарних перетворень наводять дану (ненульову) матрицю A до трапецеподібної форми, тобто до виду

B = ,

де елементи всім i = 1,2,...,k; елементи для всіх i > j та

i > k. Очевидно, що r(B) = k, тобто ранг матриці дорівнює числу ненульових рядків. Це випливає з того, що мінор порядку k матриці, розташований на перетині перших k рядків і стовпців, є визначником діагонального виду і дорівнює; а будь-який мінор порядку k+1 матриці містить нульовий рядок, а значить, дорівнює 0 (або, якщо k = n, таких мінорів немає взагалі).

Теорема.Будь-яку ненульову матрицюAрозмірностіmnможна призвести до трапецеподібної форми за допомогою елементарних перетворень.

Доведення.Оскільки A0, то існує елемент матриці
. Переставивши місцями перший і-й рядки, перший і-й стовпці, перемістимо елемент у лівий верхній кут матриці та позначимо
. Потім до рядка отриманої матриці (i= 2,3, …,m) додамо перший рядок, помножений на число . В результаті цих елементарних перетворень отримаємо матрицю

A
.

Якщо всі елементи
матриці A дорівнюють нулю, то теорема доведена. Якщо ж існує елемент
, то, перестановкою другого і i-того рядків, другого іj-того стовпців матриці A, перемістимо елемент на місце елемента і позначимо
(якщо
тоді відразу позначимо
). Потім до рядка отриманої матриці (i= 3, …,m) додамо другий рядок, помножений на число . В результаті отримаємо матрицю

.

Продовживши цей процес, за кінцеве число кроків отримаємо матрицю B, тобто наведемо матрицю як трапецеподібної формі.

приклад.Обчислимо ранг матриці



. Стрілки позначені такі елементарні перетворення: 1) переставили місцями перший і другий рядки; 2) додали до четвертого рядка третій; 3) додали до третього рядка перший, помножений на -2, і четвертий рядок поділили на 3; 4) поділили третій рядок на 5 та переставили місцями третій та четвертий рядки; 5) до третього рядка, помноженого на -3, додали другий рядок і до четвертого рядка додали третій. Видно, що матриця, отримана з матриці А вказаними елементарними перетвореннями, має трапецеподібну форму з трьома рядками. Отже, r(A) = 3.

Елементарні перетворення матриці- це перетворення матриці , у яких зберігається еквівалентність матриць. Таким чином, елементарні перетворення не змінюють безліч рішень системи лінійних рівнянь алгебри , яку представляє ця матриця.

Елементарні перетворення використовуються у методі Гауса для приведення матриці до трикутного або ступінчастого вигляду.

Визначення

Елементарними перетвореннями рядківназивають:

У деяких курсах лінійної алгебри перестановка рядків матриці не виділяється в окреме елементарне перетворення через те, що перестановку місцями будь-яких двох рядків матриці можна отримати, використовуючи множення будь-якого рядка матриці на константу k (\displaystyle k), і додаток до будь-якого рядка матриці іншого рядка, помноженого на константу k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

Аналогічно визначаються елементарні перетворення стовпців.

Елементарні перетворення оборотні.

Позначення вказує на те, що матриця A (\displaystyle A)може бути отримана з B (\displaystyle B)шляхом елементарних перетворень (чи навпаки).

Властивості

Інваріантність рангу при елементарних перетвореннях

Теорема (про інваріантність рангу при елементарних перетвореннях). Якщо A ∼ B (\displaystyle A\sim B), то r a n g A = r a n g B (\displaystyle \mathrm (rang) A=\mathrm (rang) B).

Еквівалентність СЛАУ при елементарних перетвореннях

Назвемо елементарними перетвореннями над системою лінійних рівнянь алгебри :

• перестановку рівнянь;
• множення рівняння на ненульову константу;
• складання одного рівняння з іншим, помноженим на деяку константу.

Тобто елементарні перетворення з її розширеної матрицею. Тоді справедливе наступне твердження: Нагадаємо, що дві системи називаються еквівалентними, якщо множини їх рішень збігаються.

Знаходження зворотних матриць

Теорема (про знаходження зворотної матриці). Нехай визначник матриці A n × n (\displaystyle A_(n\times n))не дорівнює нулю, нехай матриця B (\displaystyle B)визначається виразом B = [A | E ] n × 2 n (\displaystyle B=_(n\times 2n)) A (\displaystyle A). Тоді при елементарному перетворенні рядків матриці до одиничної матриці E (\displaystyle E) B (\displaystyle B)в складі до одиничної матриціодночасно відбувається перетворення до.