hogar › Instalacion y configuracion › Qué transformaciones elementales se pueden realizar con una matriz. Álgebra matricial: transformaciones elementales de matrices. Matriz, tipos de matrices, operaciones sobre matrices.

Qué transformaciones elementales se pueden realizar con una matriz. Álgebra matricial: transformaciones elementales de matrices. Matriz, tipos de matrices, operaciones sobre matrices.

Elementalconversiones de cadenas Las matrices se denominan transformaciones de los siguientes tipos:

1) Multiplicar cada elemento de una cadena por el mismo número distinto de cero. Las cadenas restantes permanecen sin cambios (en resumen: multiplicar una cadena por un número).

2) Sumar a cada elemento de una determinada línea los elementos correspondientes de otra línea, multiplicados por el mismo número. Las líneas restantes (incluida la que se está agregando) permanecen sin cambios (en resumen: agregar otra línea a una línea, multiplicada por un número).

3) Intercambie unas dos filas de la matriz. Las líneas restantes permanecen sin cambios.

Estas transformaciones se llaman respectivamente. transformaciones de la primera , segundo Y tercer tipo (algo así como ). Aplicándolos secuencialmente obtenemos transformaciones más complejas.

Definido de manera similar transformaciones de columnas elementales matrices.

Teorema

Una transformación del tercer tipo es una combinación de transformaciones del primer y segundo tipo..

Por tanto, las transformaciones del tercer tipo pueden clasificarse como más complejas que las elementales. Pero todavía se considera elemental por conveniencia.

Teorema

Cualquier matriz se puede reducir a una matriz escalonada mediante transformaciones de filas elementales.. Si aplicamos transformaciones elementales de filas y columnas a la matriz, entonces se puede reducir a una forma trapezoidal.

Por ejemplo,

á(1) Intercambiar la primera y la segunda línea (transformación del tercer tipo).

(2) La primera línea, multiplicada por 2, se sumó a la segunda y se restó de la tercera, se multiplicó por 3 y se sumó a la cuarta (transformaciones del segundo tipo).

(3) La segunda línea se restó de la tercera y la segunda línea multiplicada por 14/11 se restó de la cuarta.

(4) Intercambia la tercera y cuarta línea.ñ

Así, transformamos la matriz original.

de manera gradual

Ahora, después de haber intercambiado la segunda y tercera columna, y luego haberla intercambiado con la cuarta columna, movemos la segunda columna al lugar de la cuarta, la tercera y cuarta columnas estarán en el lugar de la segunda y tercera columna, respectivamente:

transformando así la matriz original en una trapezoidal.

Ejercicios

Lleve la matriz a formas escalonadas y trapezoidales:

Las siguientes tres operaciones se llaman transformaciones elementales de filas de matrices:

1) Multiplicación i-ésima línea matrices para el número λ ≠ 0:

que escribiremos en la forma (i) → λ(i).

2) Permutación de dos filas en una matriz, por ejemplo las filas i-ésima y k-ésima:

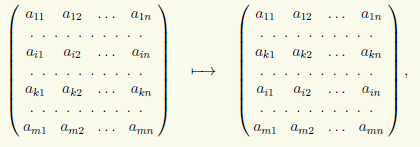
que escribiremos en la forma (i) ↔ (k).

3) Sumar a la i-ésima fila de la matriz su k-ésima fila con coeficiente λ:

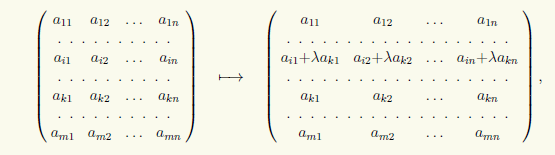
que escribiremos en la forma (i) → (i) + λ(k).

Operaciones similares en columnas de matrices se denominan transformaciones de columnas elementales.

Cada transformación elemental de las filas o columnas de una matriz tiene transformación elemental inversa, que convierte la matriz transformada en la original. Por ejemplo, la transformación inversa para permutar dos cadenas es permutar las mismas cadenas.

Cada transformación elemental de las filas (columnas) de la matriz A puede interpretarse como una multiplicación de A a la izquierda (derecha) por una matriz de forma especial. Esta matriz se obtiene si se realiza la misma transformación en matriz de identidad. Echemos un vistazo más de cerca a las conversiones de cadenas elementales.

Sea la matriz B el resultado i-ésima multiplicación filas de una matriz A de tipo m×n por el número λ ≠ 0. Entonces B = E i (λ)A, donde la matriz E i (λ) se obtiene de la matriz identidad E de orden m multiplicando su i- ésima fila por el número λ.

Sea la matriz B como resultado de la permutación de las filas i-ésima y k-ésima de la matriz A de tipo m×n. Entonces B = F ik A, donde la matriz F ik se obtiene de la matriz identidad E de orden m permutando sus filas i-ésima y k-ésima.

Sea la matriz B sumando su k-ésima fila con coeficiente λ a la i-ésima fila de una matriz A de m×n. Entonces B = G ik (λ)А, donde la matriz G ik se obtiene de la matriz identidad E de orden m sumando la k-ésima fila con el coeficiente λ a la i-ésima fila, es decir en la intersección de la i-ésima fila y la k-ésima columna de la matriz E, el elemento cero se reemplaza por el número λ.

Las transformaciones elementales de las columnas de la matriz A se implementan exactamente de la misma manera, pero al mismo tiempo se multiplica por matrices de un tipo especial no a la izquierda, sino a la derecha.

Usando algoritmos que se basan en transformaciones elementales de filas y columnas, las matrices se pueden transformar en varios tipos. Uno de los algoritmos más importantes constituye la base de la demostración del siguiente teorema.

Teorema 10.1. Usando transformaciones de filas elementales, cualquier matriz se puede reducir a vista escalonada.

◄ La demostración del teorema consiste en construir algoritmo específico llevando la matriz a una forma escalonada. Este algoritmo consiste en repetir repetidamente en un orden determinado tres operaciones asociadas a algún elemento de la matriz actual, el cual se selecciona en función de su ubicación en la matriz. En el primer paso del algoritmo, seleccionamos el superior izquierdo como elemento actual de la matriz, es decir [R] 11 .

1*. Si el elemento actual es cero, pase a la operación 2*. Si no es igual a cero, entonces la fila en la que se encuentra el elemento actual (la fila actual) se suma con los coeficientes apropiados a las filas ubicadas debajo, de modo que todos los elementos de la matriz en la columna debajo del elemento actual se vuelven cero. Por ejemplo, si el elemento actual es [A] ij, entonces como coeficiente para la k-ésima fila, k = i + 1, ..., deberíamos tomar el número - [A] kj /[A] ij. Seleccionamos un nuevo elemento actual, moviéndonos en la matriz una columna hacia la derecha y una fila hacia abajo, y procedemos al siguiente paso, repitiendo la operación 1*. Si tal cambio no es posible, es decir Se ha llegado a la última columna o fila, dejamos de transformar.

2*. Si el elemento actual en alguna fila de la matriz es igual a cero, entonces miramos los elementos de la matriz ubicados en la columna debajo del elemento actual. Si no hay ningún número distinto de cero entre ellos, procedemos a la operación 3*. Dejar entrar k-ésima línea hay un elemento distinto de cero debajo del elemento actual. Intercambiar el actual y k-ésima línea y volver a operación 1*.

3*. Si el elemento actual y todos los elementos debajo de él (en la misma columna) son iguales a cero, cambiamos el elemento actual, moviendo una columna hacia la derecha en la matriz. Si tal cambio es posible, es decir, el elemento actual no está en la columna más a la derecha de la matriz, entonces repetimos la operación 1*. Si ya hemos llegado al borde derecho de la matriz y es imposible cambiar el elemento actual, entonces la matriz tiene una forma escalonada y podemos dejar de transformarla.

Como la matriz es finita dimensiones, y en un paso del algoritmo la posición del elemento actual se desplaza hacia la derecha al menos una columna, el proceso de transformación finalizará, y en no más de n pasos (n es el número de columnas en la matriz). Esto significa que llegará un momento en que la matriz tendrá una forma escalonada.

Ejemplo 10.10. Transformemos la matriz. a forma escalonada usando transformaciones de cuerdas elementales.

Usando el algoritmo de la demostración del Teorema 10.1 y escribiendo las matrices después de completar sus operaciones, obtenemos

Transformaciones matriciales elementales- se trata de transformaciones de la matriz, como resultado de las cuales se conserva la equivalencia de las matrices. Por tanto, las transformaciones elementales no cambian el conjunto de soluciones del sistema de ecuaciones algebraicas lineales que representa esta matriz.

Las transformaciones elementales se utilizan en el método gaussiano para reducir una matriz a una forma triangular o escalonada.

Definición

Conversiones de cadenas elementales son llamados:

En algunos cursos de álgebra lineal, la permutación de filas de la matriz no se distingue como una transformación elemental separada debido al hecho de que la permutación de dos filas de la matriz se puede obtener multiplicando cualquier fila de la matriz por una constante y sumando otra fila a cualquier fila de la matriz multiplicada. por una constante , .

Definido de manera similar transformaciones de columnas elementales.

Transformaciones elementales reversible.

La notación indica que la matriz se puede obtener mediante transformaciones elementales (o viceversa).

Propiedades

Invariancia de rango bajo transformaciones elementales.

Equivalencia de SLAE bajo transformaciones elementales

Llamemos transformaciones elementales sobre un sistema de ecuaciones algebraicas lineales :

reorganizar ecuaciones;
multiplicar una ecuación por una constante distinta de cero;
sumando una ecuación a otra, multiplicada por alguna constante.

Aquellos. transformaciones elementales sobre su matriz extendida. Entonces la siguiente afirmación es verdadera: Recuerde que dos sistemas se llaman equivalentes si sus conjuntos de soluciones coinciden.

Encontrar matrices inversas

Teorema (sobre cómo encontrar la matriz inversa).
Sea el determinante de la matriz distinto de cero, dejemos que la matriz esté definida por la expresión . Luego, durante una transformación elemental de las filas de la matriz a la matriz identidad en la composición, se produce simultáneamente una transformación a.

Reducir matrices a forma escalonada

Introduzcamos el concepto de matrices escalonadas: una matriz tiene vista escalonada , si: Entonces la siguiente afirmación es verdadera:

Definiciones relacionadas

Matriz elemental. La matriz A es elemental si al multiplicar una matriz B arbitraria se obtienen transformaciones elementales de filas en la matriz B.

Literatura

Ilyin V. A., Poznyak E. G. Álgebra lineal: libro de texto para universidades. - 6ª ed., borrada. - M.: FIZMATLIT, 2004. - 280 p.

Fundación Wikimedia. 2010.

Vea qué son las “Transformaciones matriciales elementales” en otros diccionarios:

Introducción. E. Las partículas, en el sentido exacto de este término, son partículas primarias, no descomponibles, de las que, según se supone, se compone toda la materia. en moderno término de física "E. h." generalmente no se usa en su significado exacto, sino menos estrictamente para el nombre... ... Enciclopedia física

Introducción. E. Las partículas, en el sentido exacto de este término, son partículas primarias, no descomponibles, de las que, según se supone, se compone toda la materia. En el concepto de "E. h." en la física moderna la idea de entidades primordiales encuentra expresión... ... Gran enciclopedia soviética

Este término tiene otros significados, consulte Matrix. Una matriz es un objeto matemático escrito como una tabla rectangular de elementos de un anillo o campo (por ejemplo, números enteros, reales o complejos) que representa... ... Wikipedia

Una matriz es un objeto matemático escrito en forma de tabla rectangular de números (o elementos de un anillo) y que permite operaciones algebraicas (suma, resta, multiplicación, etc.) entre ella y otros objetos similares. Reglas de ejecución... ... Wikipedia

Las transformaciones elementales son las siguientes acciones sobre las filas y columnas de la matriz A:

1) intercambiar dos filas o columnas de una matriz;

2) multiplicar una fila o columna de una matriz por un número distinto de cero;

3) agregando otra fila (columna) a una fila (columna).

Teorema. Las transformaciones elementales no cambian el rango de la matriz, es decir, si la matriz B se obtiene de la matriz A mediante transformaciones elementales, entonces.

Prueba. 1). Al intercambiar dos columnas de una matriz, el número máximo de columnas linealmente independientes no cambia y, por lo tanto, su rango no cambia.

2). Deje que la matriz B se obtenga de la matriz A multiplicando la i-ésima fila por el número t0 y r(A) =k. Obviamente, cualquier menor de la matriz B que no contenga la i-ésima fila es igual al menor correspondiente de la matriz A, y cualquier menor de la matriz B que contenga la i-ésima fila es igual al menor correspondiente de la matriz A multiplicado por el número t. En consecuencia, el menor de orden k de la matriz B, correspondiente a la base menor de la matriz A, será distinto de cero, y todos los menores de orden k+1 de la matriz B, así como todos los menores de orden k+1 de la matriz A, será igual a cero. Esto significa que r(B)=k=r(A).

3). Sea la matriz B obtenida de la matriz A sumando la i-ésima fila a la j-ésima fila y r(A) = k. Los menores de orden k+1 de la matriz B que no contienen la j-ésima fila serán iguales a los menores correspondientes de la matriz A, y por tanto iguales a cero. Los menores de orden k+1 de la matriz B que contiene las filas i-ésima y j-ésima serán iguales a la suma de dos determinantes cero. Uno de estos determinantes contiene dos filas idénticas (la j-ésima fila contiene los elementos de la i-ésima fila), y el segundo determinante es menor de orden k+1 de la matriz A y, por tanto, es igual a cero. Los menores de orden k+1 de la matriz B, que contienen la j-ésima fila, pero que no contienen la i-ésima fila, serán iguales a la suma de dos menores de orden k+1 de la matriz A y por tanto también serán iguales a cero. En consecuencia, todos los menores de orden k+1 de la matriz B son iguales a 0 y r(B)k=r(A).

Deje que la matriz C se obtenga de la matriz B multiplicando la i fila por (-1). Luego, la matriz A se obtiene de la matriz C sumando la i-ésima fila a la j-ésima fila y multiplicando la i-ésima fila por (-1). Por lo tanto, como se demostró anteriormente, habrá r(A)r(C) =r(B). Así, las desigualdades r(B)r(A) y r(A)r(B) son simultáneamente válidas, lo que significa que r(A) =r(B).

Esta propiedad de las transformaciones elementales se utiliza en la práctica para calcular el rango de una matriz. Para hacer esto, usando transformaciones elementales, reducimos esta matriz A (distinta de cero) a una forma trapezoidal, es decir, a la forma

B= ,

donde elementos para todo i = 1,2,...,k; elementos para todo i > j y

yo > k. Obviamente, r (B) = k, es decir, el rango de la matriz B es igual al número de filas distintas de cero. Esto se desprende del hecho de que el menor de orden k de la matriz B, ubicado en la intersección de las primeras k filas y columnas, es un determinante diagonal y es igual a; y cualquier menor de orden k+1 de la matriz B contiene una fila cero, lo que significa que es igual a 0 (o, si k = n, no existen tales menores).

Teorema. Cualquier matriz A distinta de cero de dimensión mn se puede reducir a una forma trapezoidal mediante transformaciones elementales.

Prueba. Dado que A0, entonces existe un elemento matricial.
. Al intercambiar la primera y la i-ésima fila, la primera y la j-ésima columna, movemos el elemento a la esquina superior izquierda de la matriz y denota
. Luego a la i-ésima fila de la matriz resultante (i= 2,3, ...,m) le sumamos la primera fila multiplicada por el número . Como resultado de estas transformaciones elementales, obtenemos la matriz.

A
.

Si todos los elementos
las matrices A son iguales a cero, entonces el teorema está demostrado. Si hay un elemento
, luego, reorganizando la segunda y la i-ésima fila, la segunda y la j-ésima columna de la matriz A, movemos el elemento en lugar del elemento y denotar
(Si
, entonces inmediatamente denotamos
). Luego a la i-ésima fila de la matriz resultante (i= 3, ...,m) le sumamos la segunda fila multiplicada por el número . Como resultado obtenemos la matriz

Continuando con este proceso, en un número finito de pasos obtenemos la matriz B, es decir, reducimos la matriz A a una forma trapezoidal.

Ejemplo. Calculemos el rango de la matriz.



. Las flechas indican las siguientes transformaciones elementales: 1) se intercambiaron la primera y la segunda línea; 2) agregó una tercera a la cuarta línea; 3) sumó la primera línea, multiplicada por -2, a la tercera línea y dividió la cuarta línea por 3; 4) dividió la tercera línea entre 5 e intercambió la tercera y cuarta línea; 5) Se agregó una segunda línea a la tercera línea, multiplicada por -3, y se agregó una tercera a la cuarta línea. Se puede observar que la matriz obtenida de la matriz A mediante las transformaciones elementales indicadas tiene forma trapezoidal con tres filas distintas de cero. Por lo tanto, r(A) = 3.

Las transformaciones elementales se utilizan en el método gaussiano para reducir una matriz a una forma triangular o escalonada.

Definición

Conversiones de cadenas elementales son llamados:

En algunos cursos de álgebra lineal, la permutación de filas de la matriz no se separa en una transformación elemental separada debido al hecho de que la permutación de dos filas de la matriz se puede obtener multiplicando cualquier fila de la matriz por una constante. k (\displaystyle k), y sumando a cualquier fila de la matriz otra fila, multiplicada por una constante k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

Definido de manera similar transformaciones de columnas elementales.

Transformaciones elementales reversible.

La notación indica que la matriz A (\displaystyle A) se puede obtener de B (\displaystyle B) mediante transformaciones elementales (o viceversa).

Propiedades

Invariancia de rango bajo transformaciones elementales.

Teorema (sobre la invariancia del rango bajo transformaciones elementales).
Si A ∼ B (\displaystyle A\sim B), Eso r a n g A = r a n g B (\displaystyle \mathrm (sonó) A=\mathrm (sonó) B).

Equivalencia de SLAE bajo transformaciones elementales

Llamemos transformaciones elementales sobre un sistema de ecuaciones algebraicas lineales :

reorganizar ecuaciones;
multiplicar una ecuación por una constante distinta de cero;
sumando una ecuación a otra, multiplicada por alguna constante.

Es decir, transformaciones elementales sobre su matriz extendida. Entonces la siguiente afirmación es verdadera: Recuerde que dos sistemas se llaman equivalentes si sus conjuntos de soluciones coinciden.

Encontrar matrices inversas

Teorema (sobre cómo encontrar la matriz inversa).
Sea el determinante de la matriz. Un norte × norte (\displaystyle A_(n\times n)) no es igual a cero, sea la matriz B (\displaystyle B) está determinada por la expresión B = [A | mi ] norte × 2 norte (\displaystyle B=_(n\times 2n)). Luego, con una transformación elemental de las filas de la matriz A (\displaystyle A) a la matriz de identidad mi (\ Displaystyle E) como parte de B (\displaystyle B) La transformación ocurre al mismo tiempo. mi (\ Displaystyle E) A A − 1 (\displaystyle A^(-1)).

Popular en la categoría: