Quali trasformazioni elementari possono essere eseguite con una matrice. Algebra delle matrici: trasformazioni elementari di matrici. Matrice, tipi di matrici, operazioni sulle matrici

Elementareconversioni di stringhe le matrici sono chiamate trasformazioni dei seguenti tipi:

1) Moltiplicare ciascun elemento di una stringa per lo stesso numero diverso da zero. Le restanti righe rimangono invariate (in breve: moltiplicare una riga per un numero).

2) Aggiungendo a ciascun elemento di una certa linea gli elementi corrispondenti di un'altra linea, moltiplicati per lo stesso numero. Le restanti righe (compresa quella da aggiungere) rimangono invariate (in breve: aggiungere un'altra riga ad una riga, moltiplicata per un numero).

3) Scambia circa due righe della matrice. Le restanti linee restano invariate.

Queste trasformazioni sono chiamate rispettivamente trasformazioni del primo , secondo E terzo tipo (una specie di ). Applicandoli in sequenza, otteniamo trasformazioni più complesse.

Allo stesso modo definito trasformazioni elementari di colonne matrici.

Teorema

Una trasformazione del terzo tipo è una combinazione di trasformazioni del primo e del secondo tipo.

Pertanto, le trasformazioni del terzo tipo possono essere classificate come più complesse di quelle elementari. Ma è ancora considerato elementare per comodità.

Teorema

Qualsiasi matrice può essere ridotta a una matrice a gradini mediante trasformazioni elementari di riga. Se applichiamo trasformazioni elementari di righe e colonne alla matrice, quindi può essere ridotto a una forma trapezoidale.

Per esempio,

á(1) Scambiare la prima e la seconda riga (trasformazione del terzo tipo).

(2) La prima riga, moltiplicata per 2, è stata aggiunta alla seconda e sottratta dalla terza, moltiplicata per 3, aggiunta alla quarta (trasformazioni del secondo tipo).

(3) La seconda riga è stata sottratta dalla terza e la seconda riga moltiplicata per 14/11 è stata sottratta dalla quarta.

(4) Scambia la terza e la quarta riga.ñ

Pertanto, abbiamo trasformato la matrice originale

in modo graduale

Ora, dopo aver scambiato la seconda e la terza colonna, e poi scambiata con la quarta colonna, spostiamo la seconda colonna al posto della quarta, la terza e la quarta colonna saranno rispettivamente al posto della seconda e della terza colonna:

trasformando così la matrice originaria in una matrice trapezoidale.

Esercizi

Porta la matrice alle forme a gradini e trapezoidali:

Vengono chiamate le tre operazioni successive trasformazioni elementari di righe di matrici:

1) Moltiplicazione i-esima riga matrici per il numero λ ≠ 0:

che scriveremo nella forma (i) → λ(i).

2) Permutazione di due righe in una matrice, ad esempio la i-esima e la k-esima riga:

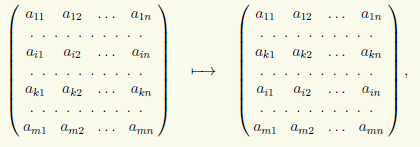
che scriveremo nella forma (i) ↔ (k).

3) Sommando alla i-esima riga della matrice la sua k-esima riga con coefficiente λ:

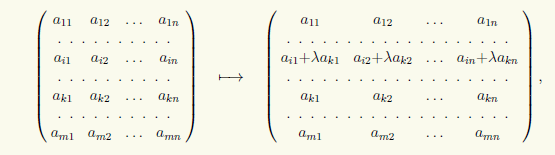
che scriveremo nella forma (i) → (i) + λ(k).

Vengono chiamate operazioni simili sulle colonne della matrice trasformazioni elementari di colonne.

Ogni trasformazione elementare delle righe o delle colonne di una matrice ha trasformazione elementare inversa, che trasforma la matrice trasformata in quella originale. Ad esempio, la trasformazione inversa per permutare due stringhe consiste nel permutare le stesse stringhe.

Ogni trasformazione elementare delle righe (colonne) della matrice A può essere interpretata come una moltiplicazione di A a sinistra (destra) per una matrice di tipo speciale. Questa matrice si ottiene se viene eseguita la stessa trasformazione su matrice identità. Diamo uno sguardo più da vicino alle conversioni di stringhe elementari.

Sia il risultato la matrice B i-esima moltiplicazione righe di una matrice A di tipo m×n per il numero λ ≠ 0. Allora B = E i (λ)A, dove la matrice E i (λ) si ottiene dalla matrice identità E di ordine m moltiplicando i suoi i- l'esima riga dal numero λ.

Sia la matrice B ottenuta come risultato della permutazione delle righe i-esima e k-esima della matrice A di tipo m×n. Allora B = F ik A, dove la matrice F ik si ottiene dalla matrice identità E di ordine m permutandone le righe i-esima e k-esima.

Sia la matrice B ottenuta sommando la sua k-esima riga con coefficiente λ alla i-esima riga di una matrice A m×n. Allora B = G ik (λ)А, dove la matrice G ik si ottiene dalla matrice identità E di ordine m sommando la k-esima riga con il coefficiente λ alla i-esima riga, cioè all'intersezione della i-esima riga e della k-esima colonna della matrice E, l'elemento zero è sostituito dal numero λ.

Le trasformazioni elementari delle colonne della matrice A sono implementate esattamente allo stesso modo, ma allo stesso tempo vengono moltiplicate per matrici di tipo speciale non a sinistra, ma a destra.

Utilizzando algoritmi basati su trasformazioni elementari di righe e colonne, è possibile trasformare le matrici vari tipi. Uno dei più importanti algoritmi di questo tipo costituisce la base della dimostrazione del seguente teorema.

Teorema 10.1. Utilizzando trasformazioni di riga elementari, qualsiasi matrice può essere ridotta a vista a gradini.

◄ La dimostrazione del teorema consiste nel costruire algoritmo specifico portando la matrice ad una forma graduale. Questo algoritmo consiste nel ripetere ripetutamente in un certo ordine tre operazioni associate a un elemento corrente della matrice, selezionato in base alla sua posizione nella matrice. Nel primo passo dell'algoritmo, selezioniamo quello in alto a sinistra come elemento corrente della matrice, cioè [A] 11 .

1*. Se l'elemento corrente è zero, vai all'operazione 2*. Se non è uguale a zero, la riga in cui si trova l'elemento corrente (la riga corrente) viene aggiunta con i coefficienti appropriati alle righe situate sotto, in modo che tutti gli elementi della matrice nella colonna sotto l'elemento corrente diventino zero. Ad esempio, se l'elemento corrente è [A] ij , allora come coefficiente per la k-esima riga, k = i + 1, ... , dovremmo prendere il numero - [A] kj /[A] ij . Selezioniamo un nuovo elemento corrente, spostandoci nella matrice di una colonna a destra e di una riga in basso, e procediamo al passo successivo, ripetendo l'operazione 1*. Se tale spostamento non è possibile, ad es. è stata raggiunta l'ultima colonna o riga, smettiamo di trasformare.

2*. Se l'elemento corrente in qualche riga della matrice è uguale a zero, esaminiamo gli elementi della matrice situati nella colonna sotto l'elemento corrente. Se tra di essi non ce ne sono di diversi da zero, si procede all'operazione 3*. Far entrare kesima riga c'è un elemento diverso da zero sotto l'elemento corrente. Scambia la corrente e kesima riga e tornare all'operazione 1*.

3*. Se l'elemento corrente e tutti gli elementi sottostanti (nella stessa colonna) sono uguali a zero, cambiamo l'elemento corrente, spostandoci di una colonna a destra nella matrice. Se tale spostamento è possibile, cioè l'elemento corrente non è nella colonna più a destra della matrice, ripetiamo l'operazione 1*. Se abbiamo già raggiunto il bordo destro della matrice e cambiare l'elemento corrente è impossibile, allora la matrice ha una forma a gradini e possiamo interrompere la trasformazione.

Poiché la matrice ha finito dimensioni, e in un passo dell'algoritmo la posizione dell'elemento corrente viene spostata a destra di almeno una colonna, il processo di trasformazione terminerà e in non più di n passi (n è il numero di colonne nella matrice). Ciò significa che arriverà il momento in cui la matrice avrà una forma a gradini.

Esempio 10.10. Trasformiamo la matrice alla forma a scaglioni utilizzando trasformazioni di stringhe elementari.

Utilizzando l'algoritmo della dimostrazione del Teorema 10.1 e scrivendo le matrici dopo aver completato le sue operazioni, otteniamo

Trasformazioni di matrici elementari- queste sono trasformazioni della matrice, a seguito delle quali viene preservata l'equivalenza delle matrici. Pertanto, le trasformazioni elementari non modificano l'insieme delle soluzioni del sistema di equazioni algebriche lineari che questa matrice rappresenta.

Le trasformazioni elementari vengono utilizzate nel metodo gaussiano per ridurre una matrice a una forma triangolare o a gradini.

Definizione

Conversioni elementari di stringhe sono chiamati:

In alcuni corsi di algebra lineare, la permutazione delle righe della matrice non viene distinta come trasformazione elementare separata poiché la permutazione di due righe qualsiasi della matrice può essere ottenuta moltiplicando qualsiasi riga della matrice per una costante e aggiungendo un'altra riga a qualsiasi riga della matrice moltiplicata da una costante , .

Allo stesso modo definito trasformazioni elementari di colonne.

Trasformazioni elementari reversibile.

La notazione indica che la matrice può essere ottenuta mediante trasformazioni elementari (o viceversa).

Proprietà

Invarianza di rango per trasformazioni elementari

Equivalenza degli SLAE sotto trasformazioni elementari

Chiamiamo trasformazioni elementari su un sistema di equazioni algebriche lineari :

• riorganizzare le equazioni;
• moltiplicare un'equazione per una costante diversa da zero;
• sommando un'equazione all'altra, moltiplicata per una costante.

Quelli. trasformazioni elementari sulla sua matrice estesa. Allora è vera la seguente affermazione: Ricordiamo che due sistemi si dicono equivalenti se i loro insiemi di soluzioni coincidono.

Trovare matrici inverse

Teorema (sulla ricerca della matrice inversa). Lascia che il determinante della matrice sia diverso da zero, lascia che la matrice sia definita dall'espressione . Quindi, durante una trasformazione elementare delle righe della matrice nella matrice identità nella composizione, avviene simultaneamente una trasformazione in.

Riduzione delle matrici alla forma a scaglioni

Introduciamo il concetto di matrici a gradini: Una matrice ha vista a gradini , se: Allora è vera la seguente affermazione:

Definizioni correlate

Matrice elementare. La matrice A è elementare se moltiplicando una matrice arbitraria B per essa si ottengono trasformazioni elementari delle righe della matrice B.

Letteratura

Ilyin V. A., Poznyak E. G. Algebra lineare: libro di testo per le università. - 6a edizione, cancellata. - M.: FIZMATLIT, 2004. - 280 p.

Fondazione Wikimedia. 2010.

Scopri cosa sono le "trasformazioni di matrici elementari" in altri dizionari:

Introduzione. Le particelle E. nel significato esatto di questo termine sono particelle primarie, ulteriori indecomponibili, da cui, per presupposto, è composta tutta la materia. Nel moderno termine fisico "E. H." solitamente usato non nel suo significato esatto, ma meno strettamente per il nome... ... Enciclopedia fisica

Introduzione. Le particelle E. nel significato esatto di questo termine sono particelle primarie, ulteriori indecomponibili, di cui, per presupposto, è composta tutta la materia. Nel concetto di "E. H." nella fisica moderna trova espressione l'idea delle entità primordiali... ... Grande Enciclopedia Sovietica

Questo termine ha altri significati, vedi Matrix. La matrice è un oggetto matematico scritto come una tabella rettangolare di elementi di un anello o campo (ad esempio numeri interi, reali o numeri complessi) che rappresenta ... ... Wikipedia

Una matrice è un oggetto matematico scritto sotto forma di una tabella rettangolare di numeri (o elementi di un anello) e che consente operazioni algebriche (addizione, sottrazione, moltiplicazione, ecc.) tra essa e altri oggetti simili. Regole per l'esecuzione... ... Wikipedia

Una matrice è un oggetto matematico scritto sotto forma di una tabella rettangolare di numeri (o elementi di un anello) e che consente operazioni algebriche (addizione, sottrazione, moltiplicazione, ecc.) tra essa e altri oggetti simili. Regole per l'esecuzione... ... Wikipedia

Una matrice è un oggetto matematico scritto sotto forma di una tabella rettangolare di numeri (o elementi di un anello) e che consente operazioni algebriche (addizione, sottrazione, moltiplicazione, ecc.) tra essa e altri oggetti simili. Regole per l'esecuzione... ... Wikipedia

Una matrice è un oggetto matematico scritto sotto forma di una tabella rettangolare di numeri (o elementi di un anello) e che consente operazioni algebriche (addizione, sottrazione, moltiplicazione, ecc.) tra essa e altri oggetti simili. Regole per l'esecuzione... ... Wikipedia

Una matrice è un oggetto matematico scritto sotto forma di una tabella rettangolare di numeri (o elementi di un anello) e che consente operazioni algebriche (addizione, sottrazione, moltiplicazione, ecc.) tra essa e altri oggetti simili. Regole per l'esecuzione... ... Wikipedia

Le trasformazioni elementari sono le seguenti azioni sulle righe e sulle colonne della matrice A:

1) scambiare due righe o colonne di una matrice;

2) moltiplicare una riga o una colonna di una matrice per un numero diverso da zero;

3) aggiungendo un'altra riga (colonna) a una riga (colonna).

Teorema. Le trasformazioni elementari non cambiano il rango della matrice, cioè se la matrice B è ottenuta dalla matrice A mediante trasformazioni elementari, allora.

Prova. 1). Quando si scambiano due colonne di una matrice, il numero massimo di colonne linearmente indipendenti non cambia e quindi il suo rango non cambia.

2). Sia la matrice B ottenuta dalla matrice A moltiplicando la riga i-esima per il numero t0 e r(A) =k. Ovviamente, qualsiasi minore della matrice B che non contiene la riga i-esima è uguale al corrispondente minore della matrice A, e qualsiasi minore della matrice B contenente la riga i-esima è uguale al corrispondente minore della matrice A moltiplicato per il numero t. Di conseguenza, il minore di ordine k della matrice B, corrispondente alla base minore della matrice A, sarà diverso da zero, e tutti i minori di ordine k+1 della matrice B, così come tutti i minori di ordine k+1 della matrice A, sarà uguale a zero. Ciò significa che r(B)=k=r(A).

3). Sia la matrice B ottenuta dalla matrice A aggiungendo la i-esima riga alla j-esima riga e r(A) = k. I minori di ordine k+1 della matrice B che non contengono la j-esima riga saranno uguali ai corrispondenti minori della matrice A, e quindi pari a zero. I minori di ordine k+1 della matrice B contenente la i-esima e la j-esima riga saranno pari alla somma di due determinanti nulli. Uno di questi determinanti contiene due righe identiche (la j-esima riga contiene gli elementi della i-esima riga), e il secondo determinante è un minore di ordine k+1 della matrice A ed è quindi uguale a zero. I minori di ordine k+1 della matrice B, contenenti la j-esima riga, ma non contenente la i-esima riga, saranno pari alla somma di due minori di ordine k+1 della matrice A e quindi saranno anch'essi pari a zero. Di conseguenza tutti i minori di ordine k+1 della matrice B sono uguali a 0 e r(B)k=r(A).

Sia la matrice C ottenuta dalla matrice B moltiplicando la riga i per (-1). Quindi la matrice A si ottiene dalla matrice C aggiungendo la riga i-esima alla riga j-esima e moltiplicando la riga i-esima per (-1). Pertanto, come dimostrato sopra, ci sarà r(A)r(C) =r(B). Pertanto le disuguaglianze r(B)r(A) e r(A)r(B) sono valide contemporaneamente, il che significa che r(A) =r(B).

Questa proprietà delle trasformazioni elementari viene utilizzata in pratica per calcolare il rango di una matrice. Per fare ciò, utilizzando trasformazioni elementari, riduciamo questa matrice A (diversa da zero) alla forma trapezoidale, cioè alla forma

B= ,

dove elementi per tutti i = 1,2,...,k; elementi per tutti i > j e

io > k. Ovviamente r(B) = k, cioè il rango della matrice B è pari al numero di righe diverse da zero. Ciò deriva dal fatto che il minore di ordine k della matrice B, posto all'intersezione delle prime k righe e colonne, è un determinante diagonale ed è uguale a; e qualsiasi minore di ordine k+1 della matrice B contiene una riga zero, il che significa che è uguale a 0 (o, se k = n, non esistono affatto tali minori).

Teorema. Qualsiasi matrice A diversa da zero di dimensione mn può essere ridotta a una forma trapezoidale utilizzando trasformazioni elementari.

Prova. Poiché A0 esiste un elemento di matrice
. Scambiando la prima e la i-esima riga, la prima e la j-esima colonna, spostiamo l'elemento nell'angolo superiore sinistro della matrice e denotare
. Quindi alla i-esima riga della matrice risultante (i= 2,3, ...,m) aggiungiamo la prima riga moltiplicata per il numero . Come risultato di queste trasformazioni elementari, otteniamo la matrice

UN
.

Se tutti gli elementi
le matrici A sono uguali a zero, allora il teorema è dimostrato. Se c'è un elemento
, quindi, riordinando la seconda e la i-esima riga, la seconda e la j-esima colonna della matrice A, spostiamo l'elemento al posto dell'elemento e denotare
(Se
, allora indichiamo immediatamente
). Quindi alla i-esima riga della matrice risultante (i= 3, ...,m) aggiungiamo la seconda riga moltiplicata per il numero . Di conseguenza, otteniamo la matrice

.

Proseguendo questo processo, in un numero finito di passaggi otteniamo la matrice B, ovvero riduciamo la matrice A ad una forma trapezoidale.

Esempio. Calcoliamo il rango della matrice



. Le frecce indicano le seguenti trasformazioni elementari: 1) la prima e la seconda riga sono state invertite; 2) aggiunto un terzo alla quarta riga; 3) ha aggiunto la prima riga, moltiplicata per -2, alla terza riga, e ha diviso la quarta riga per 3; 4) ha diviso la terza riga per 5 e ha scambiato la terza e la quarta riga; 5) alla terza riga è stata aggiunta una seconda riga, moltiplicata per -3, e alla quarta riga è stata aggiunta una terza. Si può vedere che la matrice ottenuta dalla matrice A mediante le trasformazioni elementari indicate ha forma trapezoidale con tre righe diverse da zero. Pertanto, r(A) = 3.

Trasformazioni di matrici elementari- queste sono trasformazioni della matrice, a seguito delle quali viene preservata l'equivalenza delle matrici. Pertanto, le trasformazioni elementari non modificano l'insieme delle soluzioni del sistema di equazioni algebriche lineari che questa matrice rappresenta.

Le trasformazioni elementari vengono utilizzate nel metodo gaussiano per ridurre una matrice a una forma triangolare o a gradini.

Definizione

Conversioni elementari di stringhe sono chiamati:

In alcuni corsi di algebra lineare, la permutazione delle righe della matrice non è separata in una trasformazione elementare separata poiché la permutazione di due righe qualsiasi della matrice può essere ottenuta moltiplicando qualsiasi riga della matrice per una costante k (\displaystyle k), e aggiungendo a qualsiasi riga della matrice un'altra riga, moltiplicata per una costante k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

Allo stesso modo definito trasformazioni elementari di colonne.

Trasformazioni elementari reversibile.

La notazione indica che la matrice A (\displaystyle A) può essere ottenuto da B (\displaystyle B) attraverso trasformazioni elementari (o viceversa).

Proprietà

Invarianza di rango per trasformazioni elementari

Teorema (sull'invarianza del rango per trasformazioni elementari). Se A ∼ B (\displaystyle A\sim B), Quello r un n g A = r un n g B (\displaystyle \mathrm (rang) A=\mathrm (rang) B).

Equivalenza degli SLAE sotto trasformazioni elementari

Chiamiamo trasformazioni elementari su un sistema di equazioni algebriche lineari :

• riorganizzare le equazioni;
• moltiplicare un'equazione per una costante diversa da zero;
• sommando un'equazione all'altra, moltiplicata per una costante.

Cioè trasformazioni elementari sulla sua matrice estesa. Allora è vera la seguente affermazione: Ricordiamo che due sistemi si dicono equivalenti se i loro insiemi di soluzioni coincidono.

Trovare matrici inverse

Teorema (sulla ricerca della matrice inversa). Sia il determinante della matrice A n × n (\displaystyle A_(n\times n)) non è uguale a zero, lasciamo la matrice B (\displaystyle B)è determinato dall'espressione B = [A | E] n × 2 n (\displaystyle B=_(n\times 2n)). Quindi, con una trasformazione elementare delle righe della matrice A (\displaystyle A) alla matrice identità E (\displaystyle E) nell'ambito di B (\displaystyle B) la trasformazione avviene contemporaneamente E (\displaystyle E) A UN - 1 (\displaystyle UN^(-1)).