Kādas elementāras pārvērtības var veikt ar matricu. Matricu algebra - matricu elementāras transformācijas. Matrica, matricu veidi, operācijas ar matricām
Elementārivirknes konversijas matricas sauc par šādu veidu transformācijām:
1) Katra virknes elementa reizināšana ar to pašu skaitli, kas nav nulle. Atlikušās rindas paliek nemainīgas (īsi sakot: rindas reizināšana ar skaitli).
2) Katram noteiktas rindas elementam pievienojot citas rindas atbilstošos elementus, kas reizināti ar to pašu skaitli. Pārējās rindas (tostarp pievienotā) paliek nemainīgas (īsi sakot: rindai tiek pievienota vēl viena rinda, kas reizināta ar skaitli).
3) Apmainiet dažas divas matricas rindas. Pārējās rindas paliek nemainīgas.
Šīs transformācijas sauc attiecīgi pirmās pārvērtības , otrais Un trešais veids (sava veida ). Piemērojot tos secīgi, iegūstam sarežģītākas pārvērtības.
Līdzīgi definēts elementārās kolonnas transformācijas matricas.
Teorēma
Trešā tipa transformācija ir pirmā un otrā tipa transformāciju kombinācija.
Tādējādi trešā veida transformācijas var klasificēt kā sarežģītākas nekā elementārās. Bet tas joprojām tiek uzskatīts par elementāru ērtības labad.
Teorēma
Jebkuru matricu var reducēt līdz soļu matricai, veicot elementāras rindu transformācijas. Ja matricai piemērojam elementāras rindu un kolonnu transformācijas, tad to var reducēt līdz trapecveida formai.
Piemēram,
á(1) Apmainiet pirmo un otro rindu (trešā tipa transformācija).
(2) Pirmā rinda, kas reizināta ar 2, tika pievienota otrajai un atņemta no trešās, reizināta ar 3, pievienota ceturtajai (otrā veida transformācijas).
(3) Otrā rinda tika atņemta no trešās, un otrā rinda, kas reizināta ar 14/11, tika atņemta no ceturtās.
(4) Samainīt trešo un ceturto rindu.ñ
Tādējādi mēs pārveidojām sākotnējo matricu
pakāpeniski
Tagad, apmainījuši otro un trešo kolonnu un pēc tam samainījuši to ar ceturto kolonnu, mēs pārvietojam otro kolonnu uz ceturtās kolonnas vietu, trešā un ceturtā kolonna būs attiecīgi otrās un trešās kolonnas vietā:
tādējādi pārveidojot sākotnējo matricu par trapecveida matricu.
Vingrinājumi
Novietojiet matricu pakāpienu un trapecveida formās:
Tiek izsauktas nākamās trīs darbības matricas rindu elementārās transformācijas:
1) Reizināšana i-tā rinda matricas skaitlim λ ≠ 0:
ko rakstīsim formā (i) → λ(i).
2) Matricas divu rindu, piemēram, i-tās un k-tās rindas, permutācija:
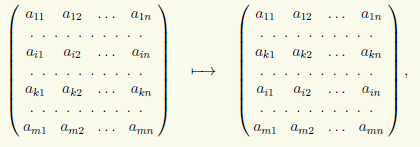
ko rakstīsim formā (i) ↔ (k).
3) Matricas i-tajai rindai pievienojot tās k-to rindu ar koeficientu λ:
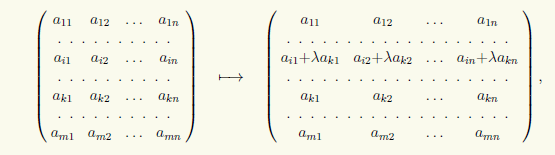
ko rakstīsim formā (i) → (i) + λ(k).
Tiek izsauktas līdzīgas operācijas ar matricas kolonnām elementārās kolonnas transformācijas.
Katrai matricas rindu vai kolonnu elementārajai transformācijai ir apgrieztā elementārā transformācija, kas pārvērš pārveidoto matricu par sākotnējo. Piemēram, apgrieztā transformācija divu virkņu permutācijai ir to pašu virkņu permutācija.
Katru matricas A rindu (kolonnu) elementāru transformāciju var interpretēt kā A reizināšanu kreisajā (labajā) ar īpašas formas matricu. Šī matrica tiek iegūta, ja tiek veikta tāda pati transformācija identitātes matrica. Sīkāk apskatīsim elementārus virkņu reklāmguvumus.
Ļaujiet matricai B būt rezultāts i-tā reizināšana m×n tipa matricas A rindas ar skaitli λ ≠ 0. Tad B = E i (λ)A, kur matricu E i (λ) iegūst no m kārtas identitātes matricas E, reizinot tās i- rinda ar skaitli λ.
Iegūsim matricu B m×n tipa matricas A i-tās un k-tās rindu permutācijas rezultātā. Tad B = F ik A, kur matricu F ik iegūst no m kārtas identitātes matricas E, permutējot tās i-to un k-to rindu.
Iegūstam matricu B, pievienojot tās k-to rindu ar koeficientu λ m × n matricas A i-tajai rindai. Tad B = G ik (λ)А, kur matricu G ik iegūst no m kārtas identitātes matricas E, i-tajai rindai pievienojot k-to rindu ar koeficientu λ, t.i. matricas E i-tās rindas un k-tās kolonnas krustpunktā nulles elements tiek aizstāts ar skaitli λ.
Matricas A kolonnu elementārās transformācijas tiek realizētas tieši tādā pašā veidā, bet tajā pašā laikā tas tiek reizināts ar īpaša veida matricām nevis kreisajā, bet labajā pusē.
Izmantojot algoritmus, kuru pamatā ir elementāras rindu un kolonnu transformācijas, matricas var pārveidot par dažādi veidi. Viens no svarīgākajiem šādiem algoritmiem veido pamatu sekojošās teorēmas pierādījumam.
Teorēma 10.1. Izmantojot elementāras rindu transformācijas, jebkuru matricu var reducēt uz pakāpju skats.
◄ Teorēmas pierādījums sastāv no konstruēšanas konkrēts algoritms matricas virzīšana pakāpeniskā formā. Šis algoritms sastāv no trīs darbību atkārtotas atkārtošanas noteiktā secībā, kas saistītas ar kādu pašreizējo matricas elementu, kas tiek izvēlēts, pamatojoties uz tā atrašanās vietu matricā. Algoritma pirmajā solī kā pašreizējo matricas elementu izvēlamies augšējo kreiso, t.i. [A] 11 .
1*. Ja pašreizējais elements ir nulle, pārejiet uz darbību 2*. Ja tas nav vienāds ar nulli, tad rinda, kurā atrodas pašreizējais elements (pašreizējā rinda), tiek pievienota ar atbilstošiem koeficientiem zemāk esošajām rindām, lai visi matricas elementi kolonnā zem pašreizējā elementa kļūtu par nulli. Piemēram, ja pašreizējais elements ir [A] ij , tad kā koeficients k-tajai rindai, k = i + 1, ... , jāņem skaitlis - [A] kj /[A] ij . Mēs izvēlamies jaunu pašreizējo elementu, matricā pārvietojot vienu kolonnu pa labi un vienu rindu uz leju, un pārejam uz nākamo soli, atkārtojot darbību 1*. Ja šāda nobīde nav iespējama, t.i. ir sasniegta pēdējā kolonna vai rinda, mēs pārtraucam transformāciju.
2*. Ja pašreizējais elements kādā matricas rindā ir vienāds ar nulli, tad mēs skatāmies cauri matricas elementiem, kas atrodas kolonnā zem pašreizējā elementa. Ja starp tiem nav skaitļu, kas atšķiras no nulles, mēs pārejam pie darbības 3*. Ielaist kth rinda zem pašreizējā elementa ir elements, kas nav nulle. Samainīt pašreizējo un kth rinda un atgriezties darbībā 1*.
3*. Ja pašreizējais elements un visi elementi zem tā (vienā kolonnā) ir vienādi ar nulli, mēs mainām pašreizējo elementu, matricā pārvietojot vienu kolonnu pa labi. Ja šāda nobīde ir iespējama, t.i., pašreizējais elements neatrodas matricas galējā labajā kolonnā, tad atkārtojam darbību 1*. Ja mēs jau esam sasnieguši matricas labo malu un pašreizējo elementu mainīt nav iespējams, tad matricai ir pakāpiena forma, un mēs varam pārtraukt transformāciju.
Tā kā matricai ir ierobežota izmēriem, un vienā algoritma solī pašreizējā elementa pozīcija tiek nobīdīta pa labi vismaz par vienu kolonnu, transformācijas process beigsies, un ne vairāk kā n soļos (n ir kolonnu skaits matricā). Tas nozīmē, ka pienāks brīdis, kad matricai būs pakāpiena forma.
Piemērs 10.10. Pārveidosim matricu 
uz ešelona formu, izmantojot elementāras virknes transformācijas.
Izmantojot algoritmu no 10.1. teorēmas pierādījuma un uzrakstot matricas pēc tās darbību pabeigšanas, iegūstam
Elementārās matricas transformācijas- tās ir matricas transformācijas, kuru rezultātā tiek saglabāta matricu ekvivalence. Tādējādi elementārās transformācijas nemaina lineāro algebrisko vienādojumu sistēmas risinājumu kopu, ko šī matrica attēlo.
Elementārās transformācijas izmanto Gausa metodē, lai reducētu matricu līdz trīsstūrveida vai pakāpiena formai.
Definīcija
Elementāra virkņu pārveidošana tiek saukti:
Dažos lineārās algebras kursos matricas rindu permutācija netiek izdalīta kā atsevišķa elementāra transformācija, jo jebkuru divu matricas rindu permutāciju var iegūt, reizinot jebkuru matricas rindu ar konstanti un pievienojot vēl vienu rindu jebkurai matricas rindai, kas reizināta. ar konstantu , .
Līdzīgi definēts elementārās kolonnas transformācijas.
Elementāras pārvērtības atgriezenisks.
Apzīmējums norāda, ka matricu var iegūt no elementārpārveidojumiem (vai otrādi).
Īpašības
Ranga invariance elementārpārveidojumos
SLAE ekvivalence elementārās transformācijās
Piezvanīsim elementāras pārvērtības lineāro algebrisko vienādojumu sistēmā :- vienādojumu pārkārtošana;
- vienādojumu reizinot ar konstanti, kas nav nulle;
- pievienojot vienu vienādojumu citam, reizinot ar kādu konstanti.
Apgriezto matricu atrašana
| Teorēma (par apgrieztās matricas atrašanu). Lai matricas determinants nav nulle, lai matrica ir definēta ar izteiksmi . Tad elementāras matricas rindu transformācijas laikā uz identitātes matricu kompozīcijā notiek transformācija uz vienlaicīgi. |
Matricu samazināšana līdz ešelona formai
Ieviesīsim soļu matricu jēdzienu: Matricai ir pakāpju skats , ja: Tad šāds apgalvojums ir patiess:Saistītās definīcijas
Elementāra matrica. Matrica A ir elementāra, ja, reizinot patvaļīgu matricu B ar to, tiek veiktas elementāras matricas B rindu transformācijas.
Literatūra
Iļjins V.A., Pozņaks E.G. Lineārā algebra: mācību grāmata universitātēm. - 6. izd., dzēsts. - M.: FIZMATLIT, 2004. - 280 lpp.
Wikimedia fonds. 2010. gads.
Skatiet, kas ir “elementārās matricas transformācijas” citās vārdnīcās:
Ievads. E. daļiņas šī termina precīzā nozīmē ir primāras, tālāk nesadalāmas daļiņas, no kurām, pieņemot, sastāv visa matērija. Mūsdienu valodā fizikas termins "E. h." parasti lieto nevis tā precīzajā nozīmē, bet mazāk stingri vārdam... ... Fiziskā enciklopēdija
Ievads. E. daļiņas šī termina precīzā nozīmē ir primāras, tālāk nesadalāmas daļiņas, no kurām, pieņemot, sastāv visa matērija. Koncepcijā "E. h." mūsdienu fizikā izpaužas priekšstats par pirmatnējām vienībām... ... Lielā padomju enciklopēdija
Šim terminam ir citas nozīmes, skatiet Matrix. Matrica ir matemātisks objekts, kas uzrakstīts kā gredzena vai lauka elementu taisnstūra tabula (piemēram, veseli skaitļi, reāli vai kompleksie skaitļi), kas attēlo ... ... Wikipedia
Matrica ir matemātisks objekts, kas uzrakstīts taisnstūrveida skaitļu tabulas (vai gredzena elementu) veidā un ļauj veikt algebriskas darbības (saskaitīšanu, atņemšanu, reizināšanu utt.) starp to un citiem līdzīgiem objektiem. Izpildes noteikumi... ... Wikipedia
Matrica ir matemātisks objekts, kas uzrakstīts taisnstūrveida skaitļu tabulas (vai gredzena elementu) veidā un ļauj veikt algebriskas darbības (saskaitīšanu, atņemšanu, reizināšanu utt.) starp to un citiem līdzīgiem objektiem. Izpildes noteikumi... ... Wikipedia
Matrica ir matemātisks objekts, kas uzrakstīts taisnstūrveida skaitļu tabulas (vai gredzena elementu) veidā un ļauj veikt algebriskas darbības (saskaitīšanu, atņemšanu, reizināšanu utt.) starp to un citiem līdzīgiem objektiem. Izpildes noteikumi... ... Wikipedia
Matrica ir matemātisks objekts, kas uzrakstīts taisnstūrveida skaitļu tabulas (vai gredzena elementu) veidā un ļauj veikt algebriskas darbības (saskaitīšanu, atņemšanu, reizināšanu utt.) starp to un citiem līdzīgiem objektiem. Izpildes noteikumi... ... Wikipedia
Matrica ir matemātisks objekts, kas uzrakstīts taisnstūrveida skaitļu tabulas (vai gredzena elementu) veidā un ļauj veikt algebriskas darbības (saskaitīšanu, atņemšanu, reizināšanu utt.) starp to un citiem līdzīgiem objektiem. Izpildes noteikumi... ... Wikipedia
Elementārās transformācijas ir šādas darbības ar matricas A rindām un kolonnām:
1) matricas divu rindu vai kolonnu maiņa;
2) matricas rindas vai kolonnas reizināšana ar skaitli, kas nav nulle;
3) citas rindas (kolonnas) pievienošana vienai rindai (kolonnai).
Teorēma. Elementārie pārveidojumi nemaina matricas rangu, tas ir, ja matricu B iegūst no matricas A ar elementārpārveidojumiem, tad.
Pierādījums. 1). Apmainot divas matricas kolonnas, maksimālais lineāri neatkarīgo kolonnu skaits nemainās, un līdz ar to nemainās arī tās rangs.
2). Ļaujiet matricu B iegūt no matricas A, reizinot i-to rindu ar skaitli t0 un r(A) =k. Acīmredzot jebkura matricas B, kas nesatur i-to rindu, ir vienāda ar matricas A atbilstošo minoro, un jebkura matricas B, kas satur i-to rindu, ir vienāda ar matricas A atbilstošo minoru, kas reizināta ar skaitli t. Līdz ar to B matricas k kārtas minors, kas atbilst matricas A pamata minoritātei, nebūs nulle, un visas matricas B kārtas k+1 minorās, kā arī visas matricas k+1 kārtas minorās. A, būs vienāds ar nulli. Tas nozīmē, ka r(B)=k=r(A).
3). Ļaujiet matricu B iegūt no matricas A, pievienojot i-to rindu j-jai rindai un r(A) = k. Matricas B kārtas k+1 minori, kas nesatur j-to rindu, būs vienādi ar atbilstošajiem matricas A minoriem un līdz ar to vienādi ar nulli. Matricas B mazākās kārtas k+1, kas satur i-to un j-to rindu, būs vienādas ar divu nulles determinantu summu. Viens no šiem determinantiem satur divas identiskas rindas (j-tajā rindā ir i-tās rindas elementi), un otrs determinants ir matricas A k+1 kārtas minors un tāpēc ir vienāds ar nulli. Matricas B mazākās kārtas k+1, kas satur j-to rindu, bet nesatur i-to rindu, būs vienādas ar divu matricas A k+1 kārtas minoritāšu summu un tāpēc arī būs vienādas ar nulle. Līdz ar to visas matricas B kārtas k+1 minorās ir vienādas ar 0 un r(B)k=r(A).
Ļaujiet matricu C iegūt no matricas B, reizinot i rindu ar (-1). Tad matricu A iegūst no matricas C, pievienojot i-to rindu j-tajai rindai un reizinot i-to rindu ar (-1). Tāpēc, kā pierādīts iepriekš, būs r(A)r(C) =r(B). Tādējādi nevienādības r(B)r(A) un r(A)r(B) ir spēkā vienlaikus, kas nozīmē, ka r(A) =r(B).
Šo elementāro pārveidojumu īpašību praksē izmanto, lai aprēķinātu matricas rangu. Lai to izdarītu, izmantojot elementāras transformācijas, mēs reducējam šo (ne nulles) matricu A līdz trapecveida formai, tas ir, līdz formai
B= 
,
kur elementi visiem i = 1,2,...,k; elementi visiem i > j un
i > k. Acīmredzot r(B) = k, tas ir, matricas B rangs ir vienāds ar rindu skaitu, kas nav nulle. Tas izriet no fakta, ka matricas B k kārtas minors, kas atrodas pirmo k rindu un kolonnu krustpunktā, ir diagonāles determinants un ir vienāds ar; un jebkurš matricas B kārtas k+1 minors satur nulles rindu, kas nozīmē, ka tā ir vienāda ar 0 (vai, ja k = n, šādu minoru nav vispār).
Teorēma. Jebkuru nulles matricu A ar izmēru mn var reducēt līdz trapecveida formai, izmantojot elementāras transformācijas.
Pierādījums. Tā kā A0, tad ir matricas elements 
. Apmainot pirmo un i-to rindu, pirmo un j-to kolonnu, mēs pārvietojam elementu 
uz matricas augšējo kreiso stūri un apzīmē 
. Tad iegūtās matricas i-tajai rindai (i= 2,3, ...,m) pievienojam pirmo rindu, kas reizināta ar skaitli 
. Šo elementāro pārveidojumu rezultātā mēs iegūstam matricu
A 
.
Ja visi elementi 
matricas A ir vienādas ar nulli, tad teorēma ir pierādīta. Ja ir elements 
, tad, pārkārtojot matricas A otro un i-to rindu, otro un j-to kolonnu, mēs pārvietojam elementu 
elementa vietā 
un apzīmē 
(Ja 
, tad uzreiz apzīmējam 
). Tad iegūtās matricas i-tajai rindai (i= 3, ...,m) pievienojam otro rindu, kas reizināta ar skaitli 
. Rezultātā mēs iegūstam matricu
.
Turpinot šo procesu, ierobežotā soļu skaitā iegūstam matricu B, tas ir, matricu A reducējam līdz trapecveida formai.
Piemērs. Aprēķināsim matricas rangu
. Bultiņas norāda uz sekojošām elementārām transformācijām: 1) tika samainīta pirmā un otrā rinda; 2) ceturtajai rindai pievienoja trešo; 3) pievienoja pirmo rindu, kas reizināta ar -2, trešajai rindai un dalīja ceturto rindu ar 3; 4) dala trešo rindu ar 5 un samainīja trešo un ceturto rindu; 5) trešajai rindai tika pievienota otrā rinda, kas reizināta ar -3, un ceturtajai rindai tika pievienota trešā. Redzams, ka no matricas A ar norādītajām elementārpārveidojumiem iegūtajai matricai ir trapecveida forma ar trim rindām, kas nav nulle. Tāpēc r(A) = 3.
Elementārās matricas transformācijas- tās ir matricas transformācijas, kuru rezultātā tiek saglabāta matricu ekvivalence. Tādējādi elementārās transformācijas nemaina lineāro algebrisko vienādojumu sistēmas risinājumu kopu, ko šī matrica attēlo.
Elementārās transformācijas izmanto Gausa metodē, lai reducētu matricu līdz trīsstūrveida vai pakāpiena formai.
Definīcija
Elementāra virkņu pārveidošana tiek saukti:
Dažos lineārās algebras kursos matricas rindu permutācija netiek izdalīta atsevišķā elementārā transformācijā, jo jebkuru divu matricas rindu permutāciju var iegūt, reizinot jebkuru matricas rindu ar konstanti. k (\displaystyle k), un jebkurai matricas rindai pievienojot vēl vienu rindu, kas reizināta ar konstanti k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).
Līdzīgi definēts elementārās kolonnas transformācijas.
Elementāras pārvērtības atgriezenisks.
Apzīmējums norāda, ka matrica A (\displaystyle A) var iegūt no B (\displeja stils B) izmantojot elementāras pārvērtības (vai otrādi).
Īpašības
Ranga invariance elementārpārveidojumos
| Teorēma (par ranga invarianci elementārpārveidojumos). Ja A ∼ B (\displaystyle A\sim B), Tas r a n g A = r a n g B (\displaystyle \mathrm (rang) A=\mathrm (rang) B). |
SLAE ekvivalence elementārās transformācijās
Piezvanīsim elementāras pārvērtības lineāro algebrisko vienādojumu sistēmā :- vienādojumu pārkārtošana;
- vienādojumu reizinot ar konstanti, kas nav nulle;
- pievienojot vienu vienādojumu citam, reizinot ar kādu konstanti.
Apgriezto matricu atrašana
| Teorēma (par apgrieztās matricas atrašanu). Ļaujiet matricas determinants A n × n (\displaystyle A_(n\times n)) nav vienāds ar nulli, ļaujiet matricai B (\displeja stils B) nosaka izteiksme B = [ A | E ] n × 2 n (\displaystyle B=_(n\times 2n)). Pēc tam ar elementāru matricas rindu transformāciju A (\displaystyle A) uz identitātes matricu E (\displaystyle E) kā daļa no B (\displeja stils B) transformācija notiek tajā pašā laikā E (\displaystyle E) Uz A – 1 (\displaystyle A^(-1)). |
