Katere osnovne transformacije lahko izvedemo z matriko. Matrična algebra - elementarne transformacije matrik. Matrika, vrste matrik, operacije na matrikah

Osnovnopretvorbe nizov matrike se imenujejo transformacije naslednjih tipov:

1) Množenje vsakega elementa niza z istim številom, ki ni nič. Preostale vrstice ostanejo nespremenjene (na kratko: množenje vrstice s številom).

2) Dodajanje vsakemu elementu določene vrstice ustreznih elementov druge vrstice, pomnoženih z istim številom. Preostale vrstice (vključno z dodano) ostanejo nespremenjene (na kratko: dodajanje druge vrstice vrstici, pomnoženo s številom).

3) Zamenjaj dve vrstici matrike. Preostale vrstice ostanejo nespremenjene.

Te transformacije se imenujejo oz preobrazbe prvega , drugo in tretja vrsta (nekako ). Če jih uporabimo zaporedno, dobimo bolj zapletene transformacije.

Podobno opredeljeno elementarne transformacije stolpcev matrice.

Izrek

Transformacija tretje vrste je kombinacija transformacij prve in druge vrste.

Tako lahko transformacije tretje vrste razvrstimo kot bolj zapletene od osnovnih. Vendar se še vedno šteje za osnovno zaradi udobja.

Izrek

Vsako matriko je mogoče zmanjšati na stopničasto matriko z osnovnimi transformacijami vrstic. Če na matriko uporabimo elementarne transformacije vrstic in stolpcev, potem ga je mogoče zmanjšati na trapezoidno obliko.

Na primer,

á(1) Zamenjaj prvo in drugo vrstico (transformacija tretje vrste).

(2) Prva vrstica, pomnožena z 2, je bila dodana drugi in odšteta od tretje, pomnožena s 3, dodana četrti (transformacije druge vrste).

(3) Druga vrstica je bila odšteta od tretje in druga vrstica, pomnožena s 14/11, je bila odšteta od četrte.

(4) Zamenjaj tretjo in četrto vrstico.ñ

Tako smo preoblikovali prvotno matriko

na postopni način

Zdaj, ko smo zamenjali drugi in tretji stolpec in ga nato zamenjali s četrtim stolpcem, premaknemo drugi stolpec na mesto četrtega, tretji in četrti stolpec se bosta pojavila na mestu drugega oziroma tretjega stolpca:

s čimer se prvotna matrika spremeni v trapezoidno.

vaje

Pripeljite matrico v stopničasto in trapezoidno obliko:

Pokličejo se naslednje tri operacije elementarne transformacije matričnih vrstic:

1) Množenje i-ta vrstica matrike za število λ ≠ 0:

ki ga bomo zapisali v obliki (i) → λ(i).

2) Permutacija dveh vrstic v matriki, na primer i-te in k-te vrstice:

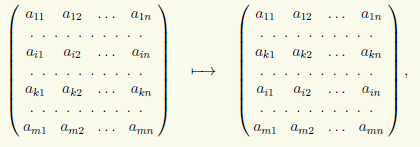
ki jih bomo zapisali v obliki (i) ↔ (k).

3) Dodajanje i-te vrstice matrike k-te vrstice s koeficientom λ:

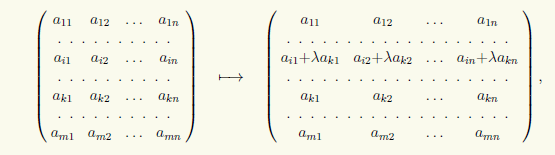
ki ga bomo zapisali v obliki (i) → (i) + λ(k).

Podobne operacije na stolpcih matrike se imenujejo elementarne transformacije stolpcev.

Vsaka osnovna transformacija vrstic ali stolpcev matrike ima inverzna elementarna transformacija, ki transformirano matriko spremeni v izvirno. Na primer, inverzna transformacija za permutacijo dveh nizov je permutacija istih nizov.

Vsako elementarno transformacijo vrstic (stolpcev) matrike A lahko interpretiramo kot množenje A na levi (desni) z matriko posebne oblike. To matriko dobimo, če izvedemo enako transformacijo identitetna matrika. Oglejmo si podrobneje osnovne pretvorbe nizov.

Naj bo rezultat matrika B i-to množenje vrstic matrike A tipa m×n s številom λ ≠ 0. Potem je B = E i (λ)A, kjer matriko E i (λ) dobimo iz identitetne matrike E reda m z množenjem njenih i- vrstico s številom λ.

Naj bo matrika B dobljena kot rezultat permutacije i-te in k-te vrstice matrike A tipa m×n. Potem je B = F ik A, kjer je matrika F ik pridobljena iz identitetne matrike E reda m s preureditvijo njene i-te in k-te vrstice.

Naj dobimo matriko B tako, da k i-ti vrstici m×n matrike A dodamo njeno k-to vrstico s koeficientom λ. Potem je B = G ik (λ)А, kjer matriko G ik dobimo iz identitetne matrike E reda m tako, da i-ti vrstici dodamo k-to vrstico s koeficientom λ, tj. na presečišču i-te vrstice in k-tega stolpca matrike E se ničelni element nadomesti s številom λ.

Elementarne transformacije stolpcev matrike A se izvajajo na popolnoma enak način, vendar se hkrati pomnoži z matricami posebne vrste ne na levi, ampak na desni.

Z uporabo algoritmov, ki temeljijo na elementarnih transformacijah vrstic in stolpcev, lahko matrike pretvorimo v različne vrste. Eden najpomembnejših takšnih algoritmov je osnova za dokaz naslednjega izreka.

Izrek 10.1. Z uporabo elementarnih transformacij vrstic je mogoče vsako matriko reducirati na stopničast pogled.

◄ Dokaz izreka je sestavljen iz konstruiranja poseben algoritem spraviti matriko v postopno obliko. Ta algoritem je sestavljen iz večkratnega ponavljanja v določenem vrstnem redu treh operacij, povezanih z nekim trenutnim elementom matrike, ki je izbran glede na njegovo lokacijo v matriki. Na prvem koraku algoritma kot trenutni element matrike izberemo zgornji levi, tj. [A] 11.

1*. Če je trenutni element enak nič, pojdite na operacijo 2*. Če ni enak nič, se vrstica, v kateri se nahaja trenutni element (trenutna vrstica), doda z ustreznimi koeficienti vrsticam, ki se nahajajo spodaj, tako da vsi elementi matrike v stolpcu pod trenutnim elementom postanejo nič. Na primer, če je trenutni element [A] ij , potem moramo kot koeficient za k-to vrstico, k = i + 1, ... vzeti število - [A] kj /[A] ij . Izberemo nov trenutni element, se v matriki premaknemo en stolpec v desno in eno vrstico navzdol ter nadaljujemo z naslednjim korakom in ponovimo operacijo 1*. Če tak premik ni mogoč, t.j. je bil dosežen zadnji stolpec ali vrstica, prenehamo s transformacijo.

2*. Če je trenutni element v neki vrstici matrike enak nič, potem pogledamo elemente matrike, ki se nahajajo v stolpcu pod trenutnim elementom. Če med njimi ni ničelnih, nadaljujemo z operacijo 3*. Spustiti noter k-ta vrstica pod trenutnim elementom je neničelni element. Zamenjajte trenutni in k-ta vrstica in vrnitev v delovanje 1*.

3*. Če so trenutni element in vsi elementi pod njim (v istem stolpcu) enaki nič, spremenimo trenutni element in premaknemo en stolpec v desno v matriki. Če je tak premik možen, tj. trenutni element ni v skrajnem desnem stolpcu matrike, ponovimo operacijo 1*. Če smo že dosegli desni rob matrike in sprememba trenutnega elementa ni mogoča, potem ima matrika stopničasto obliko in lahko prenehamo s transformacijo.

Ker ima matrika končno dimenzije in se v enem koraku algoritma položaj trenutnega elementa premakne v desno za vsaj en stolpec, se bo proces transformacije končal in v največ n korakih (n je število stolpcev v matriki). To pomeni, da bo prišel trenutek, ko bo matrica imela stopničasto obliko.

Primer 10.10. Preoblikujemo matriko v ešalonsko obliko z uporabo elementarnih transformacij nizov.

Z uporabo algoritma iz dokaza izreka 10.1 in zapisom matrik po zaključku njegovih operacij dobimo

Elementarne matrične transformacije- to so transformacije matrike, zaradi katerih se ohrani enakovrednost matrik. Tako elementarne transformacije ne spremenijo množice rešitev sistema linearnih algebrskih enačb, ki jih ta matrika predstavlja.

Elementarne transformacije se uporabljajo v Gaussovi metodi za zmanjšanje matrike na trikotno ali stopničasto obliko.

Opredelitev

Osnovne pretvorbe nizov se imenujejo:

V nekaterih tečajih linearne algebre se permutacija matričnih vrstic ne loči kot ločena elementarna transformacija zaradi dejstva, da lahko permutacijo poljubnih dveh matričnih vrstic dobimo tako, da pomnožimo katero koli matrično vrstico s konstanto in dodamo drugo vrstico kateri koli matrični vrstici, pomnoženi s konstanto,.

Podobno opredeljeno elementarne transformacije stolpcev.

Elementarne transformacije reverzibilen.

Zapis pomeni, da je matriko mogoče dobiti z elementarnimi transformacijami (ali obratno).

Lastnosti

Invariantnost ranga glede na elementarne transformacije

Ekvivalentnost SLAE pri elementarnih transformacijah

Pokličimo elementarne transformacije nad sistemom linearnih algebrskih enačb :

• preurejanje enačb;
• množenje enačbe z ničelno konstanto;
• dodajanje ene enačbe drugi, pomnoženo z neko konstanto.

Tisti. elementarne transformacije nad svojo razširjeno matriko. Potem velja naslednja izjava: Spomnimo se, da dva sistema imenujemo enakovredna, če njuni množici rešitev sovpadata.

Iskanje inverznih matrik

Izrek (o iskanju inverzne matrike). Naj bo determinanta matrike različna od nič, matriko naj definira izraz . Nato med elementarno transformacijo vrstic matrike v identitetno matriko v kompoziciji istočasno pride do transformacije v.

Zmanjšanje matrik v obliko ešalona

Predstavimo koncept stopničastih matrik: Matrika ima stopničast pogled , če: Potem velja naslednja izjava:

Sorodne definicije

Elementarna matrika. Matrika A je elementarna, če množenje poljubne matrike B z njo vodi do elementarnih transformacij vrstic v matriki B.

Literatura

Iljin V.A., Poznjak E.G. Linearna algebra: Učbenik za univerze. - 6. izd., izbrisano. - M.: FIZMATLIT, 2004. - 280 str.

Fundacija Wikimedia. 2010.

Poglejte, kaj so "elementarne matrične transformacije" v drugih slovarjih:

Uvod. E. delci v natančnem pomenu tega izraza so primarni, nadalje nerazgradljivi delci, iz katerih po predpostavki sestoji vsa snov. V sodobnem fizikalni izraz "E. h." običajno se ne uporablja v njegovem točnem pomenu, ampak manj strogo za ime... ... Fizična enciklopedija

Uvod. E. delci v natančnem pomenu tega izraza so primarni, nadalje nerazgradljivi delci, iz katerih je po predpostavki sestavljena vsa snov. V konceptu "E. h." v sodobni fiziki pride do izraza zamisel o prvobitnih entitetah ... ... Velika sovjetska enciklopedija

Ta izraz ima druge pomene, glej Matrix. Matrika je matematični objekt, zapisan kot pravokotna tabela elementov obroča ali polja (na primer cela števila, realna ali kompleksna števila), ki predstavlja ... ... Wikipedia

Matrika je matematični objekt, zapisan v obliki pravokotne tabele števil (ali elementov obroča) in omogoča algebraične operacije (seštevanje, odštevanje, množenje itd.) Med njim in drugimi podobnimi predmeti. Pravila za izvedbo... ... Wikipedia

Matrika je matematični objekt, zapisan v obliki pravokotne tabele števil (ali elementov obroča) in omogoča algebraične operacije (seštevanje, odštevanje, množenje itd.) Med njim in drugimi podobnimi predmeti. Pravila za izvedbo... ... Wikipedia

Matrika je matematični objekt, zapisan v obliki pravokotne tabele števil (ali elementov obroča) in omogoča algebraične operacije (seštevanje, odštevanje, množenje itd.) Med njim in drugimi podobnimi predmeti. Pravila za izvedbo... ... Wikipedia

Matrika je matematični objekt, zapisan v obliki pravokotne tabele števil (ali elementov obroča) in omogoča algebraične operacije (seštevanje, odštevanje, množenje itd.) Med njim in drugimi podobnimi predmeti. Pravila za izvedbo... ... Wikipedia

Matrika je matematični objekt, zapisan v obliki pravokotne tabele števil (ali elementov obroča) in omogoča algebraične operacije (seštevanje, odštevanje, množenje itd.) Med njim in drugimi podobnimi predmeti. Pravila za izvedbo... ... Wikipedia

Elementarne transformacije so naslednja dejanja na vrsticah in stolpcih matrike A:

1) zamenjava dveh vrstic ali stolpcev matrike;

2) množenje vrstice ali stolpca matrike s številom, ki ni nič;

3) dodajanje druge vrstice (stolpca) eni vrstici (stolpcu).

Izrek. Elementarne transformacije ne spremenijo ranga matrike, to je, če matriko B dobimo iz matrike A z elementarnimi transformacijami, potem.

Dokaz. 1). Pri zamenjavi dveh stolpcev matrike se največje število linearno neodvisnih stolpcev ne spremeni, zato se njen rang ne spremeni.

2). Naj matriko B dobimo iz matrike A z množenjem i-te vrstice s številom t0 in r(A) =k. Očitno je vsak minor matrike B, ki ne vsebuje i-te vrstice, enak ustreznemu minorju matrike A, vsak minor matrike B, ki vsebuje i-to vrstico, pa je enak ustreznemu minorju matrike A, pomnoženemu s številom t. Posledično bo minor reda k matrike B, ki ustreza osnovnemu minorju matrike A, različen od nič, vsi minori reda k+1 matrike B, kot tudi vsi minori reda k+1 matrike A, bo enako nič. To pomeni, da je r(B)=k=r(A).

3). Naj dobimo matriko B iz matrike A tako, da dodamo i-to vrstico j-ti vrstici in r(A) = k. Minori reda k+1 matrike B, ki ne vsebujejo j-te vrstice, bodo enaki ustreznim minorjem matrike A in torej enaki nič. Minorji reda k+1 matrike B, ki vsebuje i-to in j-to vrstico, bodo enaki vsoti dveh ničelnih determinant. Ena od teh determinant vsebuje dve enaki vrstici (j-ta vrstica vsebuje elemente i-te vrstice), druga determinanta pa je minor reda k+1 matrike A in je torej enaka nič. Minori reda k+1 matrike B, ki vsebujejo j-to vrstico, ne vsebujejo pa i-te vrstice, bodo enaki vsoti dveh manjšev reda k+1 matrike A in bodo zato enaki tudi nič. Posledično so vsi minori reda k+1 matrike B enaki 0 ​​in r(B)k=r(A).

Naj matriko C dobimo iz matrike B z množenjem vrstice i z (-1). Nato matriko A dobimo iz matrike C tako, da i-to vrstico prištejemo j-ti vrstici in i-to vrstico pomnožimo z (-1). Zato bo, kot je dokazano zgoraj, r(A)r(C) =r(B). Tako hkrati veljata neenakosti r(B)r(A) in r(A)r(B), kar pomeni, da je r(A) =r(B).

Ta lastnost elementarnih transformacij se v praksi uporablja za izračun ranga matrike. Da bi to naredili, z uporabo elementarnih transformacij reduciramo to (neničelno) matriko A na trapezoidno obliko, to je na obliko

B= ,

kjer so elementi za vse i = 1,2,...,k; elementov za vse i > j in

i > k. Očitno je r(B) = k, kar pomeni, da je rang matrike B enak številu neničelnih vrstic. To izhaja iz dejstva, da je minor reda k matrike B, ki se nahaja na presečišču prvih k vrstic in stolpcev, diagonalna determinanta in je enak; in vsak minor reda k+1 matrike B vsebuje ničelno vrstico, kar pomeni, da je enak 0 (ali, če je k = n, takšnih minorjev sploh ni).

Izrek. Vsako neničelno matriko A z dimenzijo mn lahko reduciramo na trapezoidno obliko z uporabo elementarnih transformacij.

Dokaz. Ker je A0, potem obstaja matrični element
. Z zamenjavo prve in i-te vrstice, prvega in j-tega stolpca premaknemo element v zgornji levi kot matrike in označimo
. Nato i-ti vrstici dobljene matrike (i= 2,3, ...,m) dodamo prvo vrstico, pomnoženo s številom . Kot rezultat teh elementarnih transformacij dobimo matriko

A
.

Če vsi elementi
matrike A enake nič, potem je izrek dokazan. Če obstaja element
, potem s preureditvijo druge in i-te vrstice, drugega in j-tega stolpca matrike A premaknemo element namesto elementa in označujejo
(Če
, potem takoj označimo
). Nato i-ti vrstici dobljene matrike (i= 3, ...,m) dodamo drugo vrstico, pomnoženo s številom . Kot rezultat dobimo matrico

.

Z nadaljevanjem tega procesa v končnem številu korakov dobimo matriko B, to pomeni, da matriko A reduciramo na trapezoidno obliko.

Primer. Izračunajmo rang matrike



. Puščice označujejo naslednje osnovne transformacije: 1) prva in druga vrstica sta bili zamenjani; 2) dodal tretjo četrti vrstici; 3) dodal prvo vrstico, pomnoženo z -2, tretji vrstici in četrto vrstico razdelil s 3; 4) razdelil tretjo vrstico s 5 in zamenjal tretjo in četrto vrstico; 5) drugi vrstici je bila dodana tretja vrstica, pomnožena z -3, tretja pa je bila dodana četrti vrstici. Vidimo, da ima matrika, dobljena iz matrike A z navedenimi elementarnimi transformacijami, trapezoidno obliko s tremi neničelnimi vrsticami. Zato je r(A) = 3.

Elementarne matrične transformacije- to so transformacije matrike, zaradi katerih se ohrani enakovrednost matrik. Tako elementarne transformacije ne spremenijo množice rešitev sistema linearnih algebrskih enačb, ki jih ta matrika predstavlja.

Elementarne transformacije se uporabljajo v Gaussovi metodi za zmanjšanje matrike na trikotno ali stopničasto obliko.

Opredelitev

Osnovne pretvorbe nizov se imenujejo:

V nekaterih tečajih linearne algebre permutacija matričnih vrstic ni ločena v ločeno elementarno transformacijo zaradi dejstva, da je permutacijo poljubnih dveh matričnih vrstic mogoče dobiti z množenjem katere koli matrične vrstice s konstanto k (\displaystyle k), in kateri koli vrstici matrike dodamo še eno vrstico, pomnoženo s konstanto k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).

Podobno opredeljeno elementarne transformacije stolpcev.

Elementarne transformacije reverzibilen.

Zapis pomeni, da je matrika A (\displaystyle A) je mogoče dobiti pri B (\displaystyle B) skozi elementarne transformacije (ali obratno).

Lastnosti

Invariantnost ranga glede na elementarne transformacije

Izrek (o invariantnosti ranga pod elementarnimi transformacijami). če A ∼ B (\displaystyle A\sim B), To r a n g A = r a n g B (\displaystyle \mathrm (rang) A=\mathrm (rang) B).

Ekvivalentnost SLAE pri elementarnih transformacijah

Pokličimo elementarne transformacije nad sistemom linearnih algebrskih enačb :

• preurejanje enačb;
• množenje enačbe z ničelno konstanto;
• dodajanje ene enačbe drugi, pomnoženo z neko konstanto.

To je elementarne transformacije nad njegovo razširjeno matriko. Potem velja naslednja izjava: Spomnimo se, da dva sistema imenujemo enakovredna, če njuni množici rešitev sovpadata.

Iskanje inverznih matrik

Izrek (o iskanju inverzne matrike). Naj bo determinanta matrike A n × n (\displaystyle A_(n\krat n)) ni enaka nič, naj matrika B (\displaystyle B) je določen z izrazom B = [A | E ] n × 2 n (\displaystyle B=_(n\krat 2n)). Nato z elementarno transformacijo matričnih vrstic A (\displaystyle A) na identitetno matriko E (\displaystyle E) kot del B (\displaystyle B) preobrazba se pojavi hkrati E (\displaystyle E) Za A − 1 (\displaystyle A^(-1)).