Ποιοι στοιχειώδεις μετασχηματισμοί μπορούν να πραγματοποιηθούν με έναν πίνακα. Άλγεβρα μήτρας - στοιχειώδεις μετασχηματισμοί πινάκων. Πίνακας, τύποι πινάκων, πράξεις σε πίνακες
Στοιχειώδηςμετατροπές συμβολοσειρώνΟι πίνακες ονομάζονται μετασχηματισμοί των ακόλουθων τύπων:
1) Πολλαπλασιασμός κάθε στοιχείου μιας συμβολοσειράς με τον ίδιο μη μηδενικό αριθμό. Οι υπόλοιπες συμβολοσειρές παραμένουν αμετάβλητες (εν συντομία: πολλαπλασιασμός μιας συμβολοσειράς με έναν αριθμό).
2) Προσθέτοντας σε κάθε στοιχείο μιας συγκεκριμένης σειράς τα αντίστοιχα στοιχεία μιας άλλης σειράς, πολλαπλασιαζόμενα με τον ίδιο αριθμό. Οι υπόλοιπες γραμμές (συμπεριλαμβανομένης αυτής που προστίθεται) παραμένουν αμετάβλητες (εν συντομία: προσθήκη άλλης γραμμής σε μια γραμμή, πολλαπλασιαζόμενη με έναν αριθμό).
3) Αλλάξτε μερικές δύο σειρές του πίνακα. Οι υπόλοιπες γραμμές παραμένουν αμετάβλητες.
Αυτοί οι μετασχηματισμοί ονομάζονται αντίστοιχα μεταμορφώσεις του πρώτου , δεύτερος Και τρίτου τύπου (περίπου ). Εφαρμόζοντάς τα διαδοχικά, λαμβάνουμε πιο σύνθετους μετασχηματισμούς.
Ομοίως ορίζεται στοιχειώδεις μετασχηματισμοί στηλών μήτρες.
Θεώρημα
Ένας μετασχηματισμός του τρίτου τύπου είναι κάποιος συνδυασμός μετασχηματισμών του πρώτου και του δεύτερου τύπου.
Έτσι, οι μετασχηματισμοί του τρίτου τύπου μπορούν να ταξινομηθούν ως πιο περίπλοκοι από τους στοιχειώδεις. Αλλά εξακολουθεί να θεωρείται στοιχειώδες για λόγους ευκολίας.
Θεώρημα
Οποιοσδήποτε πίνακας μπορεί να αναχθεί σε βηματικό πίνακα με μετασχηματισμούς στοιχειωδών σειρών. Αν εφαρμόσουμε στοιχειώδεις μετασχηματισμούς σειρών και στηλών στον πίνακα, τότε μπορεί να αναχθεί σε τραπεζοειδή μορφή.
Για παράδειγμα,
á(1) Αλλάξτε την πρώτη και τη δεύτερη γραμμή (μεταμόρφωση τρίτου τύπου).
(2) Η πρώτη γραμμή, πολλαπλασιασμένη με 2, προστέθηκε στη δεύτερη και αφαιρέθηκε από την τρίτη, πολλαπλασιάστηκε με 3, προστέθηκε στην τέταρτη (μετασχηματισμοί του δεύτερου τύπου).
(3) Η δεύτερη γραμμή αφαιρέθηκε από την τρίτη και η δεύτερη γραμμή πολλαπλασιασμένη με 14/11 αφαιρέθηκε από την τέταρτη.
(4) Ανταλλάξτε την τρίτη και την τέταρτη γραμμή.ñ
Έτσι, μεταμορφώσαμε τον αρχικό πίνακα
με σταδιακό τρόπο
Τώρα, αφού ανταλλάξαμε τη δεύτερη και την τρίτη στήλη και στη συνέχεια την ανταλλάξαμε με την τέταρτη στήλη, μετακινούμε τη δεύτερη στήλη στη θέση της τέταρτης, η τρίτη και η τέταρτη στήλη θα βρίσκονται στη θέση της δεύτερης και της τρίτης στήλης, αντίστοιχα:
μετατρέποντας έτσι την αρχική μήτρα σε τραπεζοειδή.
Γυμνάσια
Φέρτε τη μήτρα σε βαθμιδωτή και τραπεζοειδή μορφή:
Οι επόμενες τρεις πράξεις καλούνται στοιχειώδεις μετασχηματισμοί σειρών μήτρας:
1) Πολλαπλασιασμός i-η γραμμήπίνακες για τον αριθμό λ ≠ 0:
που θα γράψουμε με τη μορφή (i) → λ(i).
2) Μετάθεση δύο σειρών σε έναν πίνακα, για παράδειγμα της i-ης και της k-ης σειράς:
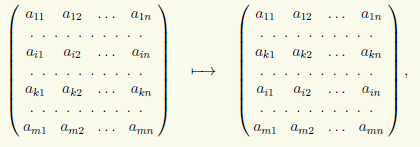
που θα γράψουμε με τη μορφή (i) ↔ (k).
3) Προσθέτοντας στην i-η σειρά του πίνακα η k-η σειρά του με συντελεστή λ:
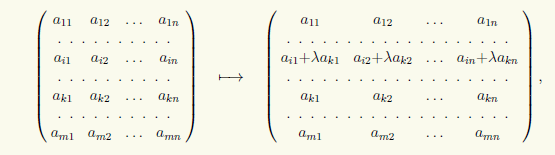
που θα γράψουμε με τη μορφή (i) → (i) + λ(k).
Παρόμοιες πράξεις σε στήλες μήτρας ονομάζονται στοιχειώδεις μετασχηματισμοί στηλών.
Κάθε στοιχειώδης μετασχηματισμός των γραμμών ή στηλών ενός πίνακα έχει αντίστροφος στοιχειώδης μετασχηματισμός, που μετατρέπει τον μετασχηματισμένο πίνακα στον αρχικό. Για παράδειγμα, ο αντίστροφος μετασχηματισμός για τη μετάθεση δύο χορδών είναι η μετάθεση των ίδιων χορδών.
Κάθε στοιχειώδης μετασχηματισμός των σειρών (στηλών) του πίνακα Α μπορεί να ερμηνευτεί ως πολλαπλασιασμός του Α στα αριστερά (δεξιά) με έναν πίνακα ειδικού τύπου. Αυτός ο πίνακας λαμβάνεται εάν εκτελεστεί ο ίδιος μετασχηματισμός μήτρα ταυτότητας. Ας ρίξουμε μια πιο προσεκτική ματιά στις στοιχειώδεις μετατροπές συμβολοσειρών.
Έστω το αποτέλεσμα του πίνακα Β i-ος πολλαπλασιασμόςσειρές ενός πίνακα A τύπου m×n με τον αριθμό λ ≠ 0. Τότε B = E i (λ)A, όπου ο πίνακας E i (λ) προκύπτει από τον πίνακα ταυτότητας E της τάξης m πολλαπλασιάζοντας το i- η σειρά με τον αριθμό λ.
Έστω ότι ο πίνακας B λαμβάνεται ως αποτέλεσμα της μετάθεσης των σειρών i-ης και k-ης του πίνακα τύπου m×n A. Τότε B = F ik A, όπου ο πίνακας F ik λαμβάνεται από τον πίνακα ταυτότητας E της τάξης m μεταθέτοντας τις i-ες και k-ες σειρές του.
Έστω ότι ο πίνακας B προκύπτει προσθέτοντας την kth σειρά του με συντελεστή λ στην i-η σειρά ενός m×n πίνακα A. Τότε B = G ik (λ)Α, όπου ο πίνακας G ik προκύπτει από τον πίνακα ταυτότητας Ε τάξης m προσθέτοντας την k-η σειρά με τον συντελεστή λ στην i-η σειρά, δηλ. στην τομή της i-ης σειράς και της k-ης στήλης του πίνακα E, το μηδενικό στοιχείο αντικαθίσταται από τον αριθμό λ.
Οι στοιχειώδεις μετασχηματισμοί των στηλών του πίνακα Α υλοποιούνται με τον ίδιο ακριβώς τρόπο, αλλά ταυτόχρονα πολλαπλασιάζονται με πίνακες ειδικού τύπου όχι στα αριστερά, αλλά στα δεξιά.
Χρησιμοποιώντας αλγόριθμους που βασίζονται σε στοιχειώδεις μετασχηματισμούς σειρών και στηλών, οι πίνακες μπορούν να μετασχηματιστούν σε διάφοροι τύποι. Ένας από τους σημαντικότερους τέτοιους αλγόριθμους αποτελεί τη βάση της απόδειξης του παρακάτω θεωρήματος.
Θεώρημα 10.1.Χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς σειρών, οποιοσδήποτε πίνακας μπορεί να αναχθεί σε κλιμακωτή όψη.
◄ Η απόδειξη του θεωρήματος συνίσταται στην κατασκευή συγκεκριμένο αλγόριθμοφέρνοντας τη μήτρα σε μια σταδιακή μορφή. Αυτός ο αλγόριθμος αποτελείται από την επανειλημμένη επανάληψη με μια ορισμένη σειρά τριών πράξεων που σχετίζονται με κάποιο τρέχον στοιχείο μήτρας, το οποίο επιλέγεται με βάση τη θέση του στον πίνακα. Στο πρώτο βήμα του αλγορίθμου, επιλέγουμε το επάνω αριστερό ως τρέχον στοιχείο του πίνακα, δηλ. [A] 11 .
1*. Εάν το τρέχον στοιχείο είναι μηδέν, μεταβείτε στη λειτουργία 2*. Αν δεν ισούται με μηδέν, τότε η σειρά στην οποία βρίσκεται το τρέχον στοιχείο (η τρέχουσα σειρά) προστίθεται με τους κατάλληλους συντελεστές στις σειρές που βρίσκονται παρακάτω, έτσι ώστε όλα τα στοιχεία μήτρας στη στήλη κάτω από το τρέχον στοιχείο να μηδενίζονται. Για παράδειγμα, εάν το τρέχον στοιχείο είναι [A] ij , τότε ως συντελεστής για την k-η σειρά, k = i + 1, ... , θα πρέπει να πάρουμε τον αριθμό - [A] kj /[A] ij . Επιλέγουμε ένα νέο τρέχον στοιχείο, μετακινούμενοι στον πίνακα μία στήλη προς τα δεξιά και μία σειρά προς τα κάτω και προχωράμε στο επόμενο βήμα, επαναλαμβάνοντας τη λειτουργία 1*. Εάν μια τέτοια μετατόπιση δεν είναι δυνατή, π.χ. έχει φτάσει η τελευταία στήλη ή σειρά, σταματάμε να μετασχηματίζουμε.
2*. Εάν το τρέχον στοιχείο σε κάποια σειρά του πίνακα είναι ίσο με μηδέν, τότε εξετάζουμε τα στοιχεία μήτρας που βρίσκονται στη στήλη κάτω από το τρέχον στοιχείο. Εάν δεν υπάρχουν μη μηδενικά μεταξύ τους, προχωράμε στη λειτουργία 3*. Αφήνω μέσα kth γραμμήυπάρχει ένα μη μηδενικό στοιχείο κάτω από το τρέχον στοιχείο. Αλλάξτε το ρεύμα και kth γραμμήκαι επιστροφή στη λειτουργία 1*.
3*. Εάν το τρέχον στοιχείο και όλα τα στοιχεία κάτω από αυτό (στην ίδια στήλη) είναι ίσα με μηδέν, αλλάζουμε το τρέχον στοιχείο, μετακινώντας μία στήλη προς τα δεξιά στον πίνακα. Εάν μια τέτοια μετατόπιση είναι δυνατή, δηλαδή το τρέχον στοιχείο δεν βρίσκεται στη δεξιά στήλη του πίνακα, τότε επαναλαμβάνουμε τη λειτουργία 1*. Εάν έχουμε ήδη φτάσει στη δεξιά άκρη του πίνακα και η αλλαγή του τρέχοντος στοιχείου είναι αδύνατη, τότε ο πίνακας έχει μια κλιμακωτή μορφή και μπορούμε να σταματήσουμε να μετασχηματίζουμε.
Αφού ο πίνακας έχει πεπερασμένο διαστάσεις, και σε ένα βήμα του αλγορίθμου η θέση του τρέχοντος στοιχείου μετατοπίζεται προς τα δεξιά κατά τουλάχιστον μία στήλη, η διαδικασία μετασχηματισμού θα τελειώσει και σε όχι περισσότερα από n βήματα (n είναι ο αριθμός των στηλών στον πίνακα). Αυτό σημαίνει ότι θα έρθει μια στιγμή που ο πίνακας θα έχει μια κλιμακωτή μορφή.
Παράδειγμα 10.10.Ας μετατρέψουμε τη μήτρα 
σε μορφή κλιμακίου χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς χορδών.
Χρησιμοποιώντας τον αλγόριθμο από την απόδειξη του Θεωρήματος 10.1 και γράφοντας τους πίνακες αφού ολοκληρώσουμε τις πράξεις του, παίρνουμε
Μετασχηματισμοί στοιχειώδους πίνακα- πρόκειται για μετασχηματισμούς του πίνακα, με αποτέλεσμα να διατηρείται η ισοδυναμία των πινάκων. Έτσι, οι στοιχειώδεις μετασχηματισμοί δεν αλλάζουν το σύνολο λύσεων του συστήματος γραμμικών αλγεβρικών εξισώσεων που αντιπροσωπεύει αυτός ο πίνακας.
Οι στοιχειώδεις μετασχηματισμοί χρησιμοποιούνται στη μέθοδο Gaussian για την αναγωγή ενός πίνακα σε τριγωνική ή βαθμιδωτή μορφή.
Ορισμός
Μετατροπές στοιχειωδών συμβολοσειρώνπου ονομάζεται:
Σε ορισμένα μαθήματα γραμμικής άλγεβρας, η μετάθεση σειρών μήτρας δεν διακρίνεται ως ξεχωριστός στοιχειώδης μετασχηματισμός λόγω του γεγονότος ότι η μετάθεση οποιωνδήποτε δύο σειρών μήτρας μπορεί να ληφθεί πολλαπλασιάζοντας οποιαδήποτε γραμμή πίνακα με μια σταθερά και προσθέτοντας μια άλλη σειρά σε οποιαδήποτε γραμμή πίνακα πολλαπλασιαζόμενο από μια σταθερά, .
Ομοίως ορίζεται στοιχειώδεις μετασχηματισμοί στηλών.
Στοιχειώδεις μεταμορφώσεις αναστρεπτός.
Ο συμβολισμός υποδεικνύει ότι ο πίνακας μπορεί να ληφθεί από στοιχειώδεις μετασχηματισμούς (ή αντίστροφα).
Ιδιότητες
Αμετάβλητο κατάταξης κάτω από στοιχειώδεις μετασχηματισμούς
Ισοδυναμία SLAE υπό στοιχειώδεις μετασχηματισμούς
Ας καλέσουμε στοιχειώδεις μετασχηματισμοί σε ένα σύστημα γραμμικών αλγεβρικών εξισώσεων :- αναδιάταξη των εξισώσεων?
- πολλαπλασιάζοντας μια εξίσωση με μια μη μηδενική σταθερά.
- προσθέτοντας μια εξίσωση στην άλλη, πολλαπλασιαζόμενη με κάποια σταθερά.
Εύρεση αντίστροφων πινάκων
| Θεώρημα (σχετικά με την εύρεση του αντίστροφου πίνακα). Έστω η ορίζουσα του πίνακα μη μηδενική, ας οριστεί ο πίνακας από την παράσταση . Στη συνέχεια, κατά τη διάρκεια ενός στοιχειώδους μετασχηματισμού των σειρών της μήτρας στη μήτρα ταυτότητας στη σύνθεση, εμφανίζεται ένας μετασχηματισμός σε ταυτόχρονα. |
Αναγωγή πινάκων σε μορφή κλιμακίου
Ας εισαγάγουμε την έννοια των βηματικών πινάκων: Ένας πίνακας έχει κλιμακωτή όψη , αν: Τότε είναι αληθής η ακόλουθη πρόταση:Σχετικοί ορισμοί
Στοιχειώδης μήτρα.Ο πίνακας Α είναι στοιχειώδης εάν πολλαπλασιάζοντας έναν αυθαίρετο πίνακα Β με αυτόν οδηγεί σε στοιχειώδεις μετασχηματισμούς των σειρών του πίνακα Β.
Βιβλιογραφία
Ilyin V. A., Poznyak E. G. Γραμμική άλγεβρα: Εγχειρίδιο για τα πανεπιστήμια. - 6η έκδ., σβησμένο. - M.: FIZMATLIT, 2004. - 280 σελ.
Ίδρυμα Wikimedia. 2010.
Δείτε τι είναι οι "στοιχειώδεις μετασχηματισμοί μήτρας" σε άλλα λεξικά:
Εισαγωγή. Τα σωματίδια Ε. με την ακριβή έννοια αυτού του όρου είναι πρωτογενή, περαιτέρω αδιάσπαστα σωματίδια, από τα οποία, κατά την υπόθεση, αποτελείται όλη η ύλη. Στο σύγχρονο φυσικής ο όρος «Ε. η." συνήθως χρησιμοποιείται όχι με την ακριβή του σημασία, αλλά λιγότερο αυστηρά για το όνομα... ... Φυσική εγκυκλοπαίδεια
Εισαγωγή. Τα σωματίδια Ε. με την ακριβή έννοια αυτού του όρου είναι πρωτεύοντα, περαιτέρω αδιάσπαστα σωματίδια, από τα οποία, κατά την υπόθεση, αποτελείται όλη η ύλη. Στην έννοια του «Ε. η." στη σύγχρονη φυσική η ιδέα των αρχέγονων οντοτήτων βρίσκει έκφραση... ... Μεγάλη Σοβιετική Εγκυκλοπαίδεια
Αυτός ο όρος έχει άλλες έννοιες, βλέπε Matrix. Το Matrix είναι ένα μαθηματικό αντικείμενο γραμμένο ως ένας ορθογώνιος πίνακας στοιχείων ενός δακτυλίου ή πεδίου (για παράδειγμα, ακέραιοι, πραγματικοί ή μιγαδικοί αριθμοί) που αντιπροσωπεύει ... ... Wikipedia
Ο πίνακας είναι ένα μαθηματικό αντικείμενο γραμμένο με τη μορφή ενός ορθογώνιου πίνακα αριθμών (ή στοιχείων ενός δακτυλίου) και επιτρέπει αλγεβρικές πράξεις (πρόσθεση, αφαίρεση, πολλαπλασιασμό κ.λπ.) μεταξύ αυτού και άλλων παρόμοιων αντικειμένων. Κανόνες για την εκτέλεση... ... Wikipedia
Ο πίνακας είναι ένα μαθηματικό αντικείμενο γραμμένο με τη μορφή ενός ορθογώνιου πίνακα αριθμών (ή στοιχείων ενός δακτυλίου) και επιτρέπει αλγεβρικές πράξεις (πρόσθεση, αφαίρεση, πολλαπλασιασμό κ.λπ.) μεταξύ αυτού και άλλων παρόμοιων αντικειμένων. Κανόνες για την εκτέλεση... ... Wikipedia
Ο πίνακας είναι ένα μαθηματικό αντικείμενο γραμμένο με τη μορφή ενός ορθογώνιου πίνακα αριθμών (ή στοιχείων ενός δακτυλίου) και επιτρέπει αλγεβρικές πράξεις (πρόσθεση, αφαίρεση, πολλαπλασιασμό κ.λπ.) μεταξύ αυτού και άλλων παρόμοιων αντικειμένων. Κανόνες για την εκτέλεση... ... Wikipedia
Ο πίνακας είναι ένα μαθηματικό αντικείμενο γραμμένο με τη μορφή ενός ορθογώνιου πίνακα αριθμών (ή στοιχείων ενός δακτυλίου) και επιτρέπει αλγεβρικές πράξεις (πρόσθεση, αφαίρεση, πολλαπλασιασμό κ.λπ.) μεταξύ αυτού και άλλων παρόμοιων αντικειμένων. Κανόνες για την εκτέλεση... ... Wikipedia
Ο πίνακας είναι ένα μαθηματικό αντικείμενο γραμμένο με τη μορφή ενός ορθογώνιου πίνακα αριθμών (ή στοιχείων ενός δακτυλίου) και επιτρέπει αλγεβρικές πράξεις (πρόσθεση, αφαίρεση, πολλαπλασιασμό κ.λπ.) μεταξύ αυτού και άλλων παρόμοιων αντικειμένων. Κανόνες για την εκτέλεση... ... Wikipedia
Οι στοιχειώδεις μετασχηματισμοί είναι οι ακόλουθες ενέργειες στις γραμμές και τις στήλες του πίνακα A:
1) εναλλαγή δύο σειρών ή στηλών ενός πίνακα.
2) πολλαπλασιασμός μιας γραμμής ή στήλης ενός πίνακα με έναν αριθμό διαφορετικό από το μηδέν.
3) προσθέτοντας μια άλλη σειρά (στήλη) σε μια σειρά (στήλη).
Θεώρημα.Οι στοιχειώδεις μετασχηματισμοί δεν αλλάζουν την κατάταξη του πίνακα, δηλαδή εάν ο πίνακας Β λαμβάνεται από τον πίνακα Α με στοιχειώδεις μετασχηματισμούς, τότε.
Απόδειξη. 1). Κατά την εναλλαγή δύο στηλών ενός πίνακα, ο μέγιστος αριθμός γραμμικά ανεξάρτητων στηλών δεν αλλάζει και επομένως η κατάταξή του δεν αλλάζει.
2). Έστω ο πίνακας B που προκύπτει από τον πίνακα A πολλαπλασιάζοντας την i-η σειρά με τον αριθμό t0 και r(A) =k. Προφανώς, κάθε ελάσσονα του πίνακα Β που δεν περιέχει την i η σειρά είναι ίση με την αντίστοιχη ελάσσονα του πίνακα Α και κάθε ελάσσονα του πίνακα Β που περιέχει την i η σειρά είναι ίση με την αντίστοιχη ελάσσονα του πίνακα Α πολλαπλασιασμένη με τον αριθμό t. Συνεπώς, η ελάσσονα τάξης k του πίνακα Β, που αντιστοιχεί στη βασική ελάσσονα του πίνακα Α, θα είναι μη μηδενική, και όλα τα ελάσσονα τάξης k+1 του πίνακα Β, καθώς και όλα τα ελάσσονα τάξης k+1 του πίνακα Α, θα ισούται με μηδέν. Αυτό σημαίνει ότι r(B)=k=r(A).
3). Έστω ότι ο πίνακας Β προκύπτει από τον πίνακα Α προσθέτοντας την i-η σειρά στην j-η σειρά και r(A) = k. Τα ελάσσονα τάξης k+1 του πίνακα Β που δεν περιέχουν την j-η σειρά θα είναι ίσα με τα αντίστοιχα ελάσσονα του πίνακα Α και επομένως ίσα με μηδέν. Οι ελάσσονες της τάξης k+1 του πίνακα Β που περιέχει τις σειρές i και j θα είναι ίσες με το άθροισμα δύο μηδενικών οριζόντων. Μία από αυτές τις ορίζουσες περιέχει δύο πανομοιότυπες σειρές (η j-η σειρά περιέχει τα στοιχεία της i-ης σειράς) και η δεύτερη ορίζουσα είναι μια ελάσσονα τάξης k+1 του πίνακα Α και επομένως είναι ίση με μηδέν. Τα ελάσσονα τάξης k+1 του πίνακα Β, που περιέχουν την j-η σειρά, αλλά δεν περιέχουν την i-η σειρά, θα είναι ίσα με το άθροισμα δύο δευτερευόντων της τάξης k+1 του πίνακα Α και επομένως θα είναι επίσης ίσα με μηδέν. Κατά συνέπεια, όλα τα ελάσσονα τάξης k+1 του πίνακα Β είναι ίσα με 0 και r(B)k=r(A).
Έστω ο πίνακας C που προκύπτει από τον πίνακα B πολλαπλασιάζοντας τη σειρά i επί (-1). Στη συνέχεια, ο πίνακας Α προκύπτει από τον πίνακα C προσθέτοντας την i-η σειρά στην j-η σειρά και πολλαπλασιάζοντας την i-η σειρά με (-1). Επομένως, όπως αποδείχθηκε παραπάνω, θα υπάρχει r(A)r(C) =r(B). Έτσι, οι ανισώσεις r(B)r(A) και r(A)r(B) ισχύουν ταυτόχρονα, που σημαίνει ότι r(A) =r(B).
Αυτή η ιδιότητα των στοιχειωδών μετασχηματισμών χρησιμοποιείται στην πράξη για τον υπολογισμό της κατάταξης ενός πίνακα. Για να γίνει αυτό, χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, ανάγουμε αυτόν τον (μη μηδενικό) πίνακα Α σε τραπεζοειδή μορφή, δηλαδή στη μορφή
Β= 
,
όπου στοιχεία για όλα τα i = 1,2,...,k; στοιχεία για όλα τα i > j και
i > k. Προφανώς, r(B) = k, δηλαδή, η κατάταξη του πίνακα B είναι ίση με τον αριθμό των μη μηδενικών σειρών. Αυτό προκύπτει από το γεγονός ότι η ελάσσονα τάξης k του πίνακα Β, που βρίσκεται στην τομή των πρώτων k σειρών και στηλών, είναι μια διαγώνια ορίζουσα και είναι ίση με; και κάθε ελάσσονα τάξης k+1 του πίνακα Β περιέχει μια μηδενική σειρά, που σημαίνει ότι είναι ίση με 0 (ή, εάν k = n, δεν υπάρχουν καθόλου τέτοιες ελάσσονες).
Θεώρημα.Οποιοσδήποτε μη μηδενικός πίνακας Α με διάσταση mn μπορεί να αναχθεί σε τραπεζοειδές σχήμα χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς.
Απόδειξη.Από το A0, τότε υπάρχει ένα στοιχείο μήτρας 
. Ανταλλάσσοντας την πρώτη και την i-η σειρά, την πρώτη και την j-η στήλη, μετακινούμε το στοιχείο 
στην επάνω αριστερή γωνία της μήτρας και δηλώνουν 
. Στη συνέχεια, στην i-η σειρά του πίνακα που προκύπτει (i= 2,3, ...,m) προσθέτουμε την πρώτη σειρά πολλαπλασιαζόμενη με τον αριθμό 
. Ως αποτέλεσμα αυτών των στοιχειωδών μετασχηματισμών, λαμβάνουμε τον πίνακα
ΕΝΑ 
.
Αν όλα τα στοιχεία 
Οι πίνακες Α είναι ίσοι με μηδέν, τότε το θεώρημα αποδεικνύεται. Αν υπάρχει κάποιο στοιχείο 
, στη συνέχεια, αναδιατάσσοντας τη δεύτερη και την i-η σειρά, τη δεύτερη και την j-η στήλη του πίνακα A, μετακινούμε το στοιχείο 
στη θέση του στοιχείου 
και δηλώνουν 
(Αν 
, τότε συμβολίζουμε αμέσως 
). Στη συνέχεια, στην i-η σειρά του πίνακα που προκύπτει (i= 3, ...,m) προσθέτουμε τη δεύτερη σειρά πολλαπλασιαζόμενη με τον αριθμό 
. Ως αποτέλεσμα, παίρνουμε τη μήτρα
.
Συνεχίζοντας αυτή τη διαδικασία, σε πεπερασμένο αριθμό βημάτων λαμβάνουμε τον πίνακα Β, δηλαδή ανάγουμε τον πίνακα Α σε τραπεζοειδές σχήμα.
Παράδειγμα.Ας υπολογίσουμε την κατάταξη του πίνακα
. Τα βέλη υποδεικνύουν τους ακόλουθους στοιχειώδεις μετασχηματισμούς: 1) η πρώτη και η δεύτερη γραμμή αντικαταστάθηκαν. 2) πρόσθεσε μια τρίτη στην τέταρτη γραμμή. 3) πρόσθεσε την πρώτη γραμμή, πολλαπλασιασμένη με -2, στην τρίτη γραμμή και διαίρεσε την τέταρτη γραμμή με 3. 4) διαίρεσε την τρίτη γραμμή με 5 και άλλαξε την τρίτη και την τέταρτη γραμμή. 5) μια δεύτερη γραμμή προστέθηκε στην τρίτη γραμμή, πολλαπλασιασμένη με -3 και μια τρίτη προστέθηκε στην τέταρτη γραμμή. Μπορεί να φανεί ότι ο πίνακας που λαμβάνεται από τον πίνακα Α με τους υποδεικνυόμενους στοιχειώδεις μετασχηματισμούς έχει τραπεζοειδές σχήμα με τρεις μη μηδενικές σειρές. Επομένως, r(A) = 3.
Μετασχηματισμοί στοιχειώδους πίνακα- πρόκειται για μετασχηματισμούς του πίνακα, με αποτέλεσμα να διατηρείται η ισοδυναμία των πινάκων. Έτσι, οι στοιχειώδεις μετασχηματισμοί δεν αλλάζουν το σύνολο λύσεων του συστήματος γραμμικών αλγεβρικών εξισώσεων που αντιπροσωπεύει αυτός ο πίνακας.
Οι στοιχειώδεις μετασχηματισμοί χρησιμοποιούνται στη μέθοδο Gaussian για την αναγωγή ενός πίνακα σε τριγωνική ή βαθμιδωτή μορφή.
Ορισμός
Μετατροπές στοιχειωδών συμβολοσειρώνπου ονομάζεται:
Σε ορισμένα μαθήματα γραμμικής άλγεβρας, η μετάθεση σειρών μήτρας δεν διαχωρίζεται σε ξεχωριστό στοιχειώδη μετασχηματισμό λόγω του γεγονότος ότι η μετάθεση οποιωνδήποτε δύο σειρών μήτρας μπορεί να ληφθεί πολλαπλασιάζοντας οποιαδήποτε γραμμή πίνακα με μια σταθερά k (\displaystyle k), και προσθέτοντας σε οποιαδήποτε σειρά του πίνακα μια άλλη σειρά, πολλαπλασιαζόμενη με μια σταθερά k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).
Ομοίως ορίζεται στοιχειώδεις μετασχηματισμοί στηλών.
Στοιχειώδεις μεταμορφώσεις αναστρεπτός.
Ο συμβολισμός υποδεικνύει ότι ο πίνακας A (\displaystyle A)μπορεί να ληφθεί από B (\displaystyle B)μέσω στοιχειωδών μετασχηματισμών (ή αντίστροφα).
Ιδιότητες
Αμετάβλητο κατάταξης κάτω από στοιχειώδεις μετασχηματισμούς
| Θεώρημα (για την αναλλοίωτη κατάταξη κάτω από στοιχειώδεις μετασχηματισμούς). Αν A ∼ B (\displaystyle A\sim B), Οτι r a n g A = r a n g B (\displaystyle \mathrm (rang) A=\mathrm (rang) B). |
Ισοδυναμία SLAE υπό στοιχειώδεις μετασχηματισμούς
Ας καλέσουμε στοιχειώδεις μετασχηματισμοί σε ένα σύστημα γραμμικών αλγεβρικών εξισώσεων :- αναδιάταξη των εξισώσεων?
- πολλαπλασιάζοντας μια εξίσωση με μια μη μηδενική σταθερά.
- προσθέτοντας μια εξίσωση στην άλλη, πολλαπλασιαζόμενη με κάποια σταθερά.
Εύρεση αντίστροφων πινάκων
| Θεώρημα (σχετικά με την εύρεση του αντίστροφου πίνακα). Έστω η ορίζουσα του πίνακα A n × n (\displaystyle A_(n\times n))δεν είναι ίσο με μηδέν, έστω ο πίνακας B (\displaystyle B)καθορίζεται από την έκφραση B = [ A | E ] n × 2 n (\displaystyle B=_(n\φορές 2n)). Στη συνέχεια, με έναν στοιχειώδη μετασχηματισμό των σειρών του πίνακα A (\displaystyle A)στον πίνακα ταυτότητας E (\displaystyle E)ως μέρος του B (\displaystyle B)η μεταμόρφωση γίνεται ταυτόχρονα E (\displaystyle E)Προς την A − 1 (\displaystyle A^(-1)). |
